When does the tangent line to the sine curve pass through the origin?

Question

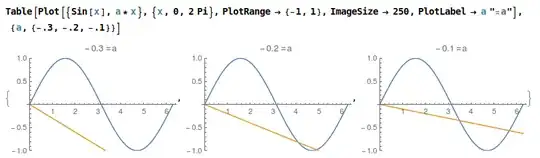
I am trying to find values $a$ and $w$ for which the line $y=ax$ is tangent to the curve $y=\sin(x)$ at $x=w$.

One immediate solution is $a=1$ and $w=0$, but I would like $a<0$ and $w\in (\pi,3\pi/2)$, and I am having a hard time finding such a solution. Asking Mathematica doesn't help (Solve, Reduce, Minimize all say This system cannot be solved) and asking Google gives me elementary calculus problems. Here is a picture showing such values of $a$ and $w$ exist (and giving an impression of how the problem changes with $a$ changing):

It is clear that there is some $a\in(-.3,-.2)$ such that $y=ax$ is tangent to $\sin(x)$, and I could find a numerical approximation, but I want an exact solution.

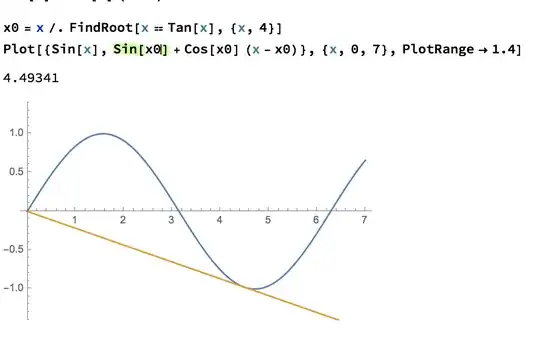
Thought 1: Describe the tangent line to $\sin(x)$ at $(w,\sin(w))$ as $y=\sin(w)+\cos(w)(x-w)$, and find when that intersects the origin. This leads to solving the equation $\tan(w)=w$, seemingly impossible.

Thought 2: Given $a$, I can find a spot on the sine curve with slope $a$. Indeed, such a point is $\cos(w)=a$, or $w=\arccos(a)$. Due to the limited range of $\arccos$ and wanting $w\in (\pi,3\pi/2)$, I need $w=2\pi-\arccos(a)$. Now I have to solve $a(2\pi-\arccos(a))=\sin(2\pi-\arccos(a))$, which can be simplified by the periodicity of $\sin$ and knowing $\sin(\arccos(a))=\sqrt{1-a^2}$, but that doesn't help too much.

My problem is actually slightly more general, I have the curve $y=\sin(cx)$ for some changing $c$. I know there exists exactly one triple $(a,c,w)$, for $a<0$ and $w\in (\pi/c, 3\pi/2c)$ such that $y=ax$ is tangent to $y=\sin(cx)$ at $x=w$, but I am worried this is a problem that cannot be solved. I tried doing this in the (seemingly) simplest case $c=1$ above, but to no avail. I would be very glad to know if there are related problems / solutions / approaches.

Answer 1

As already said in answers and comments, there is no explicit solution to the equation $x=\tan(x)$; this is already tha case for $x=\cos(x)$ and numerical methods are required.

However, you can have very good numerical approximations using Padé approximants, that is to say writing $$f(x)=\tan(x)-x \approx \frac {P_n(x)}{Q_m(x)}$$ where $P_n(x)$ and $Q_m(x)$ are polynomials of preselected degrees $n$ and $m$. When this is done, we just need to solve for $x$ $P_n(x)=0$. For sure, the developments need to be done around $x=\frac{3\pi}2$.

For example, using $n=1$ and $m=1$ would give $$P_1(x)=-\frac{3}{2} \pi \left(x-\frac{3 \pi }{2}\right)-1\implies x=\frac{9 \pi ^2-4}{6 \pi }\approx 4.500182$$

Using $n=2$ and $m=1$ would give $$P_2(x)=-\frac{2}{3} \left(x-\frac{3 \pi }{2}\right)^2-\frac{3}{2} \pi \left(x-\frac{3 \pi }{2}\right)-1\implies x=\frac{6 \pi +\sqrt{324 \pi ^2-384}1}{16} $$ which is $\approx 4.493398$ while the numerical solution would be $\approx 4.493409$.

Using $n=2$ and $m=3$ would give $$P_2(x)=\frac{1}{80} \left(9 \pi ^2-56\right) \left(x-\frac{3 \pi }{2}\right)^2-\frac{57}{40} \pi \left(x-\frac{3 \pi }{2}\right)-1$$ which would lead to $$x=\frac{-216 \pi +108 \pi ^3-\sqrt{254016 \pi ^2-286720}}{72 \pi ^2-448}\approx 4.493409 $$ which is the numerical solution for seven significant figures.

Edit

I you prefer to avoid radicals,we can consider $x_m$ as the solution of $P_1(x)$ for various $m$. The first terms are given below $$\left( \begin{array}{ccc} m & x_m & \approx \\ 1 & \frac{-4+9 \pi ^2}{6 \pi } & 4.500182390 \\ 2 & \frac{3 \pi \left(-20+27 \pi ^2\right)}{2 \left(-8+27 \pi ^2\right)} & 4.500182390 \\ 3 & \frac{32-252 \pi ^2+243 \pi ^4}{6 \pi \left(-16+27 \pi ^2\right)} & 4.493404773 \\ 4 & \frac{81 \pi \left(16-60 \pi ^2+45 \pi ^4\right)}{2 \left(112-1080 \pi ^2+1215 \pi ^4\right)} & 4.493408901 \\ 5 & \frac{-448+7296 \pi ^2-17820 \pi ^4+10935 \pi ^6}{2 \pi \left(992-4320 \pi ^2+3645 \pi ^4\right)} & 4.493409379 \\ 6 & \frac{\pi \left(-34304+244944 \pi ^2-442260 \pi ^4+229635 \pi ^6\right)}{2 \left(-2176+41328 \pi ^2-113400 \pi ^4+76545 \pi ^6\right)} & 4.493409454 \\ 7 & \frac{8704-242112 \pi ^2+1070496 \pi ^4-1530900 \pi ^6+688905 \pi ^8}{2 \pi \left(-25600+205632 \pi ^2-408240 \pi ^4+229635 \pi ^6\right)} & 4.493409458 \end{array} \right)$$

Answer 2

The tangent to a function $f$ a point $x_0$ has the equation $$y=f(x_0)+f'(x_0)(x-x_0)$$ which can be rewritten as $$y=f(x_0)-f'(x_0)+f'(x_0)x\ .$$ Thus, the intercept with the $y$ axis is at $y=f(x_0)-f'(x_0)$. Therefore, finding tangents that pass through the origin is equivalent to finding roots of the function $g(x)=f-xf'$. In your case $f(x)=\sin(x)$ so you need to find a solution to $$\sin(x)-x\cos(x)=0\ ,$$ or equivalently, $$x=\tan(x)\ .$$ This can be easily done in Mathematica:

Answer 3

well, as already pointed out, the $x$ values of the intersection points solve $x = \tan x.$ There are infinitely many such points, you are asking about the first one with $x > 0.$ The slope $a = \cos x.$