I have a function
$$U = 2A\{\alpha, \beta\} + 3B\{\beta,\gamma\} + 4\alpha$$
where $\alpha, \beta, \gamma$ are exogenous parameters and with curly brackets I mean a functional dependence (that is, $A$ depends from $\alpha$ and $\beta$ and $B$ depends from $\beta$ and $\gamma$).
I has been told that the partial derivative $\frac {\partial U} {\partial \alpha} $ is $2A_\alpha + 4$.
But shouldn't be that the total derivative? I thought that partial derivatives account only for direct effects, so that $\frac {\partial U} {\partial \alpha} $ should be simply $4$.
UPDATED: In the comments I have got that $2A_\alpha + 4\alpha$ should be considered as the partial derivative, not the total one. However in the book "Fundamental methods of Mathematical Economics" of Chiang it is written:
Finding the Total Derivative
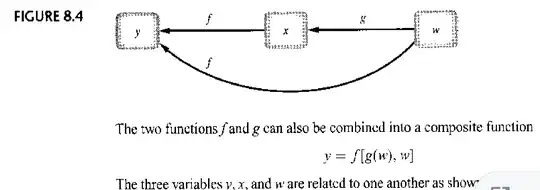
To carry on the discussion in a general framework, let us consider any function $y=f(x,w)$ where $x=g(w)$.
The two functions $f$ and $g$ can also be combined into a composite function $y=f[g(w),w]$.
The three variables $y$, $x$, and $w$ are related to one another as shown in Fig. 8.4. In this figure, which we shall refer to as channel map, it is clearly seen that $w$ - the ultimate source of change- can affect $y$ through two separate channels: (1) indirectly, via the function $g$ and then $f$ (the straight arrows), and (2) directly, via the function $f$ (the curved arrow). The direct effect can simply be represented by the partial derivative $f_w$. But the indirect effect can only be expressed by a product of two derivatives, $f_x \frac{dx}{dw}$ , or $\frac{\partial y}{\partial x} \frac{dx}{dy}$, by the chain rule for a composite function. Adding up the two effects gives us the desired total derivative of $y$ with respect to $w$:
$$\frac{dy}{dw} = f_x \frac{dx}{dw} + f_w = \frac{\partial y}{\partial x} \frac{dx}{dw} + \frac{\partial y} {\partial w}$$
According to the Chiang book hence in this case the partial derivative $\frac{\partial U}{\partial \alpha}$ should be just 4, while the total derivative $\frac{dU}{d\alpha}$ should be $2A_\alpha + 4$.
So, who is right?