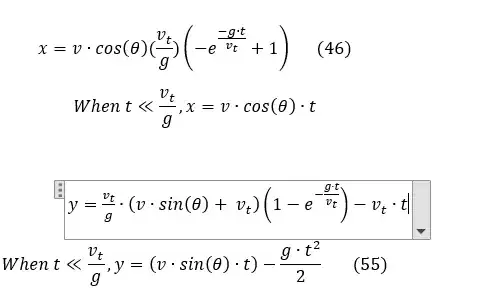0

How can I simplify the top equation in the picture to the lower equation in the picture when the condition $t \ll \frac{v_t}g$ applies. I dont seem to understand the logic behind it :( Thank you for your help!

enter image description here

Noble Mushtak
  • 18,869
Noobcoder
  • 55

3 Answers3

2

The $\ll$ symbol means $t$ is much smaller than $\frac{v_t}{g}$. To learn more about this, check out this Math.SE question.

Noble Mushtak
  • 18,869
  • Yes sorry, I corrected it. I put the wrong picture – Noobcoder Oct 23 '16 at 10:13
  • @Noobcoder Now, I am still having trouble understanding their derivation. I think someone else on this site will likely be better at understanding this than me since I am not that good at physics. Sorry! – Noble Mushtak Oct 23 '16 at 13:46
0

I suppose that $t$ here is supposed to be positive. It seems that the "simplification" being made here is $$ e^{-g t/v_t}\approx 1- g t/v_t $$ Notably, this is a good approximation whenever $g t/v_t \ll 1$, which is to say that $t\ll v_t/g$.

Ben Grossmann
  • 234,171
  • 12
  • 184
  • 355
0

The equation follows if you use a Taylor expansion to order 2:

$$ 1 - e^{\frac{-gt}{v_t}} \approx \frac{gt}{v_t} - \frac{1}{2} \frac{g^2t^2}{v^2_t} + O\Big(\Big( \frac{gt}{v_t}\Big)^3\Big) $$

You just have to slash off a remaining term
$$ -\frac{1}{2} \frac{g}{v_t} t^2 <<-\frac{1}{2}t << -\frac{1}{2} \frac{v_t}{g}. $$

Now, what does it all mean? This is just the ballistic problem in a low velocity, high drag setting:

You have, for vertical motion, the equilibrium condition for the force

$$ mg = kv_t \iff v_t = \frac {mg} {k} $$

Actually $\ \ v_{\infty} \ \ $ would be a better name.

Now, from the equations of motion

$$ m \ddot {x} = - k \dot {x}, \ \ \ \ \ \ \ \ \ \ \ \dot {x}(0) = v\cos(\theta) $$ $$ m \ddot {y} = k \dot {y} - mg, \ \ \ \ \dot {y}(0) = v\sin(\theta) $$

you get your solutions, which, for a short flight time $$ t << \frac{v_t}{g} $$ reduces to the familiar drag-less equations.

Luca
  • 785