1

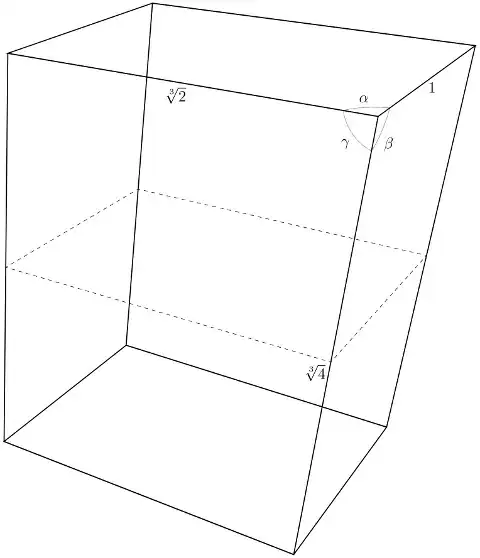
The defining property of the A series paper is that when a sheet of paper (represented by a rectangle) is cut in half, both of the resulting rectangles are similar to the original one.

Are there any other shapes or solids that have this property?

Google is silent.

user376034
  • 611

2 Answers2

2

A rectangular parallelepiped with sides in the ratio $1 \times \sqrt[3]{2} \times \sqrt[3]{4}$ has this property (when cut by the bisecting plane orthogonal to the long side).

Having an "A-side" rectangular base doesn't work: Bisecting the volume must result in a scaling by $1/\sqrt[3]{2} = 2^{-1/3}$, not $1/\sqrt{2} = 2^{-1/2}$.

Edit: Yes, there are others.

  • Every parallelogram with sides of length $1$ and $\sqrt{2}$ (not just a rectangle) is split into two self-similar copies by the line bisecting the long sides (and parallel to the short sides). (Incidentally, the resulting halves are oppositely-oriented to the original because bisecting reverses the roles of "long side" and "short side" at the acute angles. That is, the pieces must be reflected, not just rotated and scaled, to be made congruent to the original.)

  • The same idea works with non-rectangular parallelepipeds, but care is required with the angles between edges. The parallelepiped shown is bisected in volume by the dashed plane, but the pieces not self-similar unless there exists a vertex at which the interior angles of the incident faces are equal: $\alpha = \beta = \gamma$:

    Since interior angles of a parallelogram come in pairs $\alpha$, $\pi - \alpha$, we may assume without loss of generality that each of $\alpha$, $\beta$, $\gamma$ does not exceed a right angle. For convenience, call these the acute angles of a parallelepiped. (Note that in this usage, one or more "acute" angles may be right angles.)

    If the acute angles are equal and $v$ is a vertex meeting three acute angles, there is an axis $\ell$ through $v$ making equal angles with each incident edge, and a one-third rotation about $\ell$ cyclically permutes the edges so that each each maps to an edge $\sqrt[3]{2}$ times as long: $\frac{1}{2}\sqrt[3]{4} \to 1 \to \sqrt[3]{2} \to \sqrt[3]{4}$. (Note, incidentally, that the pieces have the same orientation as the original. This is a manifestation of the "personality split" between even-dimensional and odd-dimensional Cartesian spaces: An $n$-cycle is an even permutation if and only if $n$ is odd.)

    If the acute angles are not all equal, the halves are not similar to the whole: Up to similarity, a parallelepiped is uniquely specified by the ratios of the edge lengths (in fixed order $a < b < c$, say shortest to longest, with the shortest being unity) and its acute angles (in some compatible order, say $\alpha = \angle ab$, $\beta = \angle ac$, $\gamma = \angle bc$, as shown).

A non-rectangular parallelepiped with self-similar halves

  • I haven't checked carefully, but if an "object" can be disconnected, it appears there are examples homeomorphic to a product of Cantor sets, obtained (in the plane, for example) from affine maps of the type $$ \left[\begin{array}{@{}c@{}} x \\ y \\ \end{array}\right] \mapsto \left[\begin{array}{@{}c@{}} -\frac{1}{\sqrt{2}}y \pm 1 \\ \frac{1}{\sqrt{2}}x \\ \end{array}\right]. $$ (These map the rectangle $[-\sqrt{2}, \sqrt{2}] \times [-1, 1]$ onto its left and right halves by the obvious rotation, scaling, and translation.)
Community
  • 1
Andrew D. Hwang
  • 82,053
0

In fact, this property completely defines the ratio height/width which is $\sqrt{2}$

Why $\sqrt{2}$? Let us write that ratio Height/Width is preserved while halving the rectangle gives the relationship:

$$\frac{H}{W} \ = \ \frac{W}{H/2}$$

(don't forget that the old width becomes the new height).

Otherwise said:

$$\frac{H}{W} \ = \ \frac{2W}{H}$$

which is equivalent to $H^2=2W^2$. Thus $\dfrac{H}{W}=2$, from which:

$$\dfrac{H}{W}=\sqrt{2}$$

Jean Marie
  • 88,997