Is "square inversion" possible?

Question

So, there exists in geometry circle inversion:

Can I perform a similar "inversion" technique through a square?

What would, for example, a square look like when inverted through another square?

Answer 1

When you ask, "Can I perform a similar 'inversion' through a square?", the answer is "yes", in the sense that you can define "inversion in a square" however you like! The issue is not whether the definition articulates some kind of Platonic, a priori aspect of inversion, it's whether the definition is useful for categorizing and investigating phenomena.

The definition implicit in your figure does not seem to have a natural generalization to a square, but inversion in a circle has another characterization: If $C$ is a circle of center $O$ and radius $r > 0$, and if $P \neq O$ is a point, the image $P'$ of $P$ under inversion in $C$ is the point lying on the ray $OP$ and satisfying $|OP|\, |OP'| = r^{2}$.

You might therefore proceed like so: If $O$ is a point, and if $C$ is a curve that intersects each ray through $O$ exactly once, and if $P \neq O$, then we might define $P'$, the image of $P$ under inversion in $C$, to be the point lying on the ray $OP$ and satisfying $|OP|\, |OP'| = |OC|^{2}$, with $OC$ denoting the distance from $O$ to $C$ along the ray $OP$.

In polar coordinates centered at $O$, if $C$ is the polar graph $r = f(\theta)$ for some $2\pi$-periodic function $f$, then the point $P$ with polar coordinates $(R, \theta)$ maps to the point $P'$ with polar coordinates $(f(\theta)^{2}/R, \theta)$.

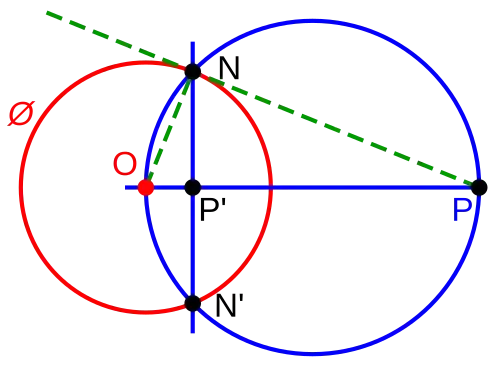
Here, for example, is the image (blue) of a circle under inversion in a square in the preceding sense, taking $O$ to be the center of the square: