Find all values of $a$ such that the function $\, f(x) = x^3 + ax^2 + 3x - 1\,$ is always increasing on $\mathbb R.$
$\ f'(x) = 3x^2 + 2ax + 3.$
For $f$ to be increasing, $\,f'(x) $ must be greater than $ 0.$
Therefore, $ a\gt -\dfrac{3(x^2+1)}{2x}.$
Is this correct?
In order for $y^\prime=3x^2+2ax+3$ to be positive for any $x$ the graph cannot intersect the $x$-axis which means that the discriminant
$$ b^2-4ac=4a^2-36$$
must be negative. Therefore
$$ -3<a<3$$
You should think about whether dividing by x was actually allowed. Remember that x could be 0, since you need that inequality to hold for all real x. For $3x^2+2ax+3$ to be above the x axis, it cannot have any real roots. So it must have this quantity $b^2-4ac$ (the discriminant) be negative. You know what b and c are and you can solve for a.
For $f_a$ to be increasing, $\,f_a'(x) $ must be greater than $ 0.$
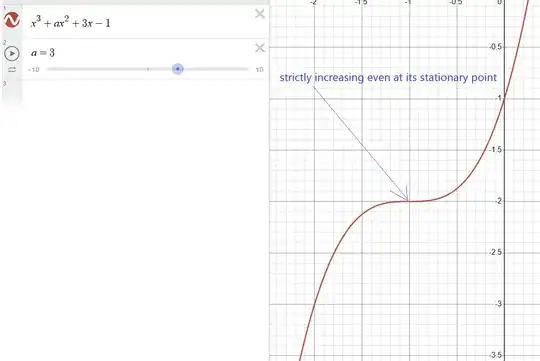
No: observe that $x^3$ is strictly (always) increasing yet has slope $0$ at $0.$ The fact is:
for a differentiable function $f$ to be strictly increasing, its derivative $f'$ just needs to be nonnegative on its domain.
(The converse of course isn't universally true.)
Find all values of $a$ such that the function $\, f_a(x) = x^3 + ax^2 + 3x - 1\,$ is always increasing on $\mathbb R.$
$\ f_a'(x) = 3x^2 + 2ax + 3.$
Noting that $f_a'$ is a smiley parabola with discriminant $(2a)^2-4(3)(3)=4(a^2-9),$ \begin{align}&f_a \text{ is strictly increasing on }\mathbb R\\\implies&f_a'\text{ is nonnegative on }\mathbb R\\\iff& f_a'\text{ never crosses the $x$-axis}\\\iff &4(a^2-9)\le0\\\iff&-3\le a\le3.\end{align}
Now, take any $a$ in $[-3,3];$ from the above, $f_a'$ is nonnegative on $\mathbb R$ and equals $0$ (at most once, so) only at isolated points, therefore, $f_a$ is strictly increasing on $\mathbb R.$
Hence, the function $f_a$ is strictly increasing precisely when $a\in[-3,3]$.
$\ f_a'(x) = 3x^2 + 2ax + 3.$
For $f_a$ to be increasing, $\,f_a'(x) $ must be greater than $ 0.$
Therefore, $ a\gt -\dfrac{3(x^2+1)}{2x}.$
No, the parameter $a$ and the variable $x$ are independent of each other, and the condition on $f_a'$ applies over its entire domain.
