Prove $\int_0^{\infty}\frac{\ln (x)}{(x^2+1)(x^3+1)}\ dx=-\frac{37}{432}\pi^2$ with real method

Question

I came across the following integral: $$\large{\int_0^\infty \frac{\ln (x)}{(x^2+1)(x^3+1)}\ dx=-\frac{37}{432}\pi^2}$$ I know it could be solved with resuide method, and I want to know if there are some real methods can sove it? Meanwhile,I remember a similar integral: $$\large{\int_0^\infty \frac{1}{(x^2+1)(x^a+1)}\ dx=\frac{\pi}{4}}$$ And I want to know the following one: $${\color{red}{\large{\int_0^\infty \frac{\ln x}{(x^2+1)(x^a+1)}\ dx = \huge{?}}}}$$ Using the Mathematica I got the follow result.

Could you suggest some ideas how to prove this? Any hints will be appreciated.

Answer 1

A real-analytic technique may be to exploit $$ I = \int_0^1 \frac{1-x^3}{(1+x^2)(1+x^3)}\log(x)\,dx $$ then expand $f(x)=\frac{1-x^3}{(1+x^2)(1+x^3)}$ as a Taylor series around $x=0$, $$ f(x) = \sum_{n\geq 0}\left(1-x^2-2 x^3+x^4+2 x^5+x^6-2 x^7-x^8 + x^{10} \right) x^{12n} $$ and exploit $$ \int_0^1 x^k\log(x)\,dx = -\frac{1}{(k+1)^2} $$ to convert $I$ into a combination of Dirichlet $L$-functions $L(s,\chi)$ where $s=2$ and $\chi$ is a Dirichlet character $\!\!\pmod{12}$, or a combination of trigamma functions evaluated at multiples of $\frac{1}{12}$: the reflection formula for $\psi'$ is helpful, since it gives $$ \sum_{n\geq 0}\left(\frac{1}{(12n+1)^2}+\frac{1}{(12n+11)^2}\right) = \frac{2+\sqrt{3}}{36}\,\pi^2,$$ $$ \sum_{n\geq 0}\left(\frac{1}{(12n+3)^2}+\frac{1}{(12n+9)^2}\right)=\frac{1}{72}\,\pi^2,$$ $$ \sum_{n\geq 0}\left(\frac{1}{(12n+4)^2}+\frac{1}{(12n+8)^2}\right)=\frac{1}{108}\,\pi^2,$$ $$ \sum_{n\geq 0}\left(\frac{1}{(12n+5)^2}+\frac{1}{(12n+7)^2}\right)=\frac{2-\sqrt{3}}{36}\,\pi^2,$$ $$ \sum_{n\geq 0}\frac{1}{(12n+6)^2}=\frac{1}{288}\pi^2.$$ To deduce $I=\color{red}{-\frac{37}{432}\pi^2}$ is now just a matter of simple algebra.

Answer 2

Preliminary Result:

$\displaystyle \frac{2}{(x^2+1)(x^3+1)} \equiv \frac{x+1}{x^2+1}-\frac{x^2+x-1}{x^3+1}$

Proof: Obvious.

Consider the parametrised integral:

$\displaystyle f(\alpha) = \int \frac{x^\alpha \, \text{d}x}{(x^2+1)(x^3+1)} = \frac{1}{2} \int \frac{x^{\alpha+1}+x^\alpha}{x^2+1}-\frac{x^{\alpha+2}+x^{\alpha+1}-x^\alpha}{x^3+1} \, \text{d}x$

For the first part, substitute $t = x^2$, and $t = x^3$ for the second part

$\displaystyle f(\alpha) = \frac{1}{4} \int_0^\infty \frac{t^{\frac{\alpha}{2}}+t^\frac{\alpha-1}{2}}{1+t} \text{d}t +\frac{1}{6}\int_0^\infty \frac{t^{\frac{\alpha}{3}}+t^{\frac{\alpha-1}{3}}-t^{\frac{\alpha-2}{3}}}{1+t} \text{d}t$

Use the Integral Representations of the Beta Function to obtain:

$\displaystyle f(\alpha) = \frac{\text{B}(1+\frac{\alpha}{2},-\frac{\alpha}{2})+\text{B}(\frac{1+\alpha}{2},\frac{1-\alpha}{2})}{4} - \ \frac{\text{B}(1+\frac{\alpha}{3},-\frac{\alpha}{3})+\text{B}(\frac{2+\alpha}{3},\frac{1-\alpha}{3})-\text{B}(\frac{1+\alpha}{3},\frac{2-\alpha}{3})}{6}$

$\displaystyle \frac{f(\alpha)}{\pi} = \frac{\csc{\left(\pi+\frac{\pi \alpha}{2} \right)}+\csc{\left(\frac{\pi}{2}+\frac{\pi \alpha}{2}\right)}}{4}-\frac{\csc{\left( \pi + \frac{\pi \alpha}{3} \right)}+\csc{\left(\frac{2\pi}{3} +\frac{\pi \alpha}{3}\right)}-\csc{\left( \frac{\pi}{3} + \frac{\pi \alpha}{3}\right)}}{6}$

$\displaystyle \frac{12f(\alpha)}{\pi} = 3\sec{\frac{\pi \alpha}{2}} -3\csc{\frac{\pi \alpha}{2}}+2\csc{\frac{\pi \alpha}{3}}+2\csc{\left( \frac{2\pi}{3}+\frac{\pi \alpha}{3}\right)}-2\csc{\left(\frac{\pi}{3}+\frac{\pi \alpha}{3}\right)}$

Differentiate both sides with respect to $\alpha$ and evaluate at $0$ to obtain the integral you want.

Answer 3

Let's define the branch of $\log$ to lie on the posive real axis. We consider the complex valued function

$$ f(z)=\frac{\log(z)^2}{(z^2+1)(z^3+1)} $$

we integrate this function around a keyhole contour in the complex plane with slit at the positive real axis. The contributions from the big circle will vanish out because $f(|z|)\sim \log(|z|)/|z|^5$ as $|z|\rightarrow \infty$ so we are left with

$$ \oint f(z)=\int_0^{\infty}\frac{\log(x)^2}{(x^2+1)(x^3+1)}-\int_0^{\infty}\frac{(\log(x)+2 i \pi)^2}{(x^2+1)(x^3+1)}=2\pi i\sum_i\text{Res}(f(z),z=z_i) $$

where are the roots of the denominator of $f(z)$: $z_0=-1,z_{2/3}=\pm i,z_{4,5}=e^{\pm i2 \pi/3}$. We can rewrite this as $$ \int_0^{\infty}\frac{\log(x)}{(x^2+1)(x^3+1)}=\sum_i\text{Res}(f(z),z=z_i)-2\pi i\int_0^{\infty}\frac{1}{(x^2+1)(x^3+1)} $$

The remaining integral can be evaluated either by cumbersome partial fraction decomposition or by considering

$$ g(z)=\frac{\log(z)}{(z^2+1)(z^3+1)} $$

integrated around the same contour then above.

I leave the details to you but from now on (also the calculation of residues if one keep in mind $\log(i)=\frac{i\pi}{2},\log(i)=\frac{3i\pi}{2}$ for this choice of branchcut) so i leave the details to you...

As an alternative the remaining integral might be ignored because it will yield a purely imaginary contribution and we can write (the lhs is purely real)

$$ \int_0^{\infty}\frac{\log(x)}{(x^2+1)(x^3+1)}=\Re\left[\sum_i\text{Res}(f(z),z=z_i)\right] $$

---

This method will work for

$$ \int_0^{\infty}\frac{\log(z)^2}{(z^2+1)(z^n+1)}dz $$

as long $n$ is a natural number

Answer 4

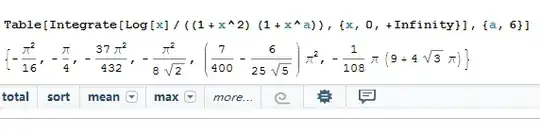
Here is a variant of @tired's solution. In this solution, you are only required to know:

• How to expand a rational function into partial fraction decomposition,
• How to compute complex logarithm, and
• The following claim:

Claim. For any $z \in \Bbb{C}\setminus(-\infty, 0]$ we have $$ I(z) := \int_{0}^{\infty} \left( \frac{\log x}{x+z} - \frac{\log x}{x+1} \right) \, dx = -\frac{1}{2}\log^2 z \tag{1}$$ where $\log$ is the principal value of the complex logarithm.

---

Computation. Before proving the claim, let us see how $\text{(1)}$ allows us to compute the integral in question. Using the partial fraction decomposition, we get

\begin{align*} \frac{1}{(1+x^2)(1+x^3)} &= \frac{1-i}{4} \cdot\frac{1}{x-i} + \frac{1+i}{4}\cdot\frac{1}{x+i} \\ &\qquad \qquad + \frac{1}{6}\cdot \frac{1}{x+1} - \frac{1}{3}\cdot \frac{1}{x - e^{\pi i/3}} - \frac{1}{3}\cdot \frac{1}{x - e^{-\pi i/3}}. \end{align*}

(Obviously this is a disguise of @tired's complex-analytic solution, since this decomposition often comes from residue computation. On the other hand, residue is no longer a necessity and thus one can work purely with algebra.)

Also notice that the sum of 'coefficients' are zero: $ \frac{1-i}{4} + \frac{1+i}{4} + \frac{1}{6} - \frac{1}{3} - \frac{1}{3} = 0$. Therefore it follows from the claim that

\begin{align*} \int_{0}^{\infty} \frac{\log x}{(1+x^2)(1+x^3)} \, dx &= \frac{1-i}{4} I(-i) + \frac{1+i}{4}I(i)\\ &\qquad \qquad + \frac{1}{6}I(1) - \frac{1}{3}I(-e^{\pi i/3}) - \frac{1}{3}I(-e^{-\pi i/3}) \\ &= -\frac{1}{2} \bigg[ \frac{1-i}{4} \left( -\frac{i\pi}{2} \right)^2 + \frac{1+i}{4}I\left( \frac{i\pi}{2} \right)^2 \\ &\qquad \qquad + 0 - \frac{1}{3}\left( -\frac{2i\pi}{3} \right)^2 - \frac{1}{3}\left( \frac{2i\pi}{3} \right)^2 \bigg] \\ &= -\frac{37}{432}\pi^2. \end{align*}

---

Proof of Claim. Now it remains to compute the integral $\text{(1)}$ This is easily done by differentiating $I(z)$:

$$ I'(z) = - \int_{0}^{\infty} \frac{\log x}{(x+z)^2} \, dx. $$

In order to compute this integral, we first replace the lower limit by $\epsilon > 0$ to obtain

$$ - \int_{\epsilon}^{\infty} \frac{\log x}{(x+z)^2} \, dx = \frac{\epsilon \log \epsilon}{z(z+\epsilon)} - \frac{1}{z}\log (z+\epsilon). $$

Taking limit as $\epsilon \to 0^+$, we get

$$ I'(z) = -\frac{1}{z}\log z, \qquad I(1) = 0. $$

This is enough to prove the claim. ////

Answer 5

\begin{align} &\int_0^\infty\frac{\ln x}{(1+x^2)(1+x^3)}\,dx\\ =&\int_0^1 \frac{(1-x^3)\ln x}{(1+x^2)(1+x^3)}\,dx =\int_0^1 \ln x\ d\bigg[\ln\frac{(1+x) (1+x^2)^{\frac12}}{(1+x^3) ^{\frac23}}\bigg]\\ \overset{ibp}=&\ \frac23\int_0^1\frac{\ln(1+x^3)}x\overset{x^3\to x}{dx} -\frac12\int_0^1\frac{\ln(1+x^2)}x \overset{x^2\to x}{dx}-\int_0^1\frac{\ln(1+x)}xdx\\ =&\ \left(\frac29–\frac14-1 \right) \int_0^1\frac{\ln(1+x)}xdx=\left(-\frac{37}{36}\right)\frac{\pi^2}{12}=-\frac{37\pi^2}{432} \end{align} where $\int_0^1\frac{\ln(1+x)}xdx=\frac{\pi^2}{12} $

Answer 6

\begin{align}J&=\int_0^{\infty}\frac{\ln x}{(x^2+1)(x^3+1)}\ dx\\ &=\int_0^1\frac{\ln x}{(x^2+1)(x^3+1)}\ dx+\underbrace{\int_1^{\infty}\frac{\ln x}{(x^2+1)(x^3+1)}\ dx}_{u=\frac1x}\\ &=\int_0^1\frac{\ln x}{(x^2+1)(x^3+1)}\ dx-\int_0^1\frac{u^3\ln u}{(u^2+1)(u^3+1)}\ du\\ &=\underbrace{\int_0^1\frac{x\ln x}{1+x^2}dx}_{u=x^2}+\frac13\int_0^1\frac{\ln x}{1+x}dx-\frac23\underbrace{\int_0^1\frac{(2x-1)\ln x}{x^2-x+1}dx}_{\text{IBP}}\\ &=\frac14\int_0^1\frac{\ln u}{1+u}du+\frac13\int_0^1\frac{\ln x}{1+x}dx-\frac23\underbrace{\Big[\ln(x^2-x+1)\ln x\Big]_0^1}_{=0}+\\ &\frac23\int_0^1\frac{\ln(x^2-x+1)}{x}dx\\ &=\frac7{12}\int_0^1\frac{\ln x}{1+x}dx+\frac23\int_0^1\frac{\ln\left(\frac{1+x^3}{1+x}\right)}{x}dx\\ &=\frac7{12}\int_0^1\frac{\ln x}{1+x}dx+\frac23\underbrace{\int_0^1\frac{\ln(1+x^3)}{x}dx}_{u=x^3}-\frac23\int_0^1\frac{\ln(1+x)}{x}dx\\ &=\frac7{12}\int_0^1\frac{\ln x}{1+x}dx+\frac29\int_0^1\frac{\ln(1+u)}{u}du-\frac23\int_0^1\frac{\ln(1+x)}{x}dx\\ &=\frac7{12}\int_0^1\frac{\ln x}{1+x}dx-\frac49\underbrace{\int_0^1\frac{\ln(1+x)}{x}dx}_{\text{IBP}}=\frac7{12}\int_0^1\frac{\ln x}{1+x}dx+\frac49\int_0^1\frac{\ln x}{1+x}dx\\ &=\frac{37}{36}\int_0^1\frac{\ln x}{1+x}dx=\frac{37}{36}\int_0^1\frac{\ln x}{1-x}dx-\frac{37}{36}\underbrace{\int_0^1\frac{2x\ln x}{1-x^2}dx}_{u=x^2}\\ &=\frac{37}{36}\int_0^1\frac{\ln x}{1-x}dx-\frac{37}{72}\int_0^1\frac{\ln u}{1-u}du=\frac{37}{72}\int_0^1\frac{\ln x}{1-x}dx\\ &=\frac{37}{72}\times -\frac{\pi^2}{6}=\boxed{-\frac{37\pi^2}{432}} \end{align} NB: I assume that $\displaystyle\int_0^1\frac{\ln x}{1-x}dx=-\frac{\pi^2}{6}$