11

Here is a theorem from Kuipers-Neiderreiter:

If $\{ x_n \}$ is a sequence uniformly distributed mod 1, then $\overline{\lim} n |x_{n+1} - x_n| = \infty$

I'm not 100% sure what this means so let's put an equidistibuted sequence $\{ n^2 \sqrt{2}\}$ (or any irrational number, $\sqrt{7}$ etc) the theorem says: $$ \limsup \hspace{0.0625in}n\; \Big| \;\{ (n+1)^2 \sqrt{2}\} - \{ n^2 \sqrt{2}\}\;\Big| = \infty $$

The proof would proceed by contradiction. If the limsup were finite...

  • $ | e^{2 \sqrt{2}\pi i \, (n+1)^2} - e^{2 \sqrt{2}\pi i \, n^2} | \leq 2\pi \Big| \;\{ (n+1)^2 \sqrt{2}\} - \{ n^2 \sqrt{2}\}\;\Big| = O(\frac{1}{N}) $

Weyl's equidistribution has that the average is zero:

  • $\displaystyle \frac{1}{N} \sum_{n=0}^{N-1} e^{2\pi i \, n^2\sqrt{2} } \to 0$

And by the Littlewood Tauberian Theorem $e^{2\pi i \, n^2 \sqrt{2}}\to 0$ but these numbers all have magnitude $1$.

Littlewood Theorem If $\sum a_n x^n \to s$ as $x \to 1$ and $a_n = O(\frac{1}{n})$ then $\sum a_n \to s$

This argument

  • is a proof by contradiction
  • uses a Tauberian theorem
  • does not use any features of the sequence $\{ n^2 \sqrt{2}\}$

is there an alternative proof that is more direct? That is not by contradiction or does not use Tauberian theory?

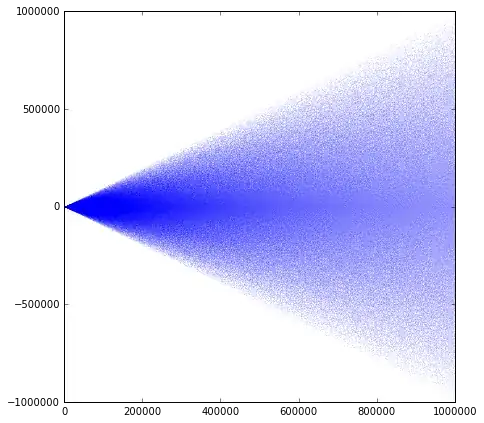
enter image description here

A plot of $n \, \big( \{(n+1)^2 \sqrt{2}\} - \{ n^2 \sqrt{2}\} \big) $ for $0 < n < 10^6$.

Alex Ravsky
  • 106,166
cactus314
  • 25,084

2 Answers2

3

One have $(n+1)^2=n^2+2n+1$ and so $\{(n+1)^2\sqrt 2\}= \{\{n^2\sqrt2\}+\{(2n+1)\sqrt2\}\}$. $\{(n+1)^2\sqrt 2\}$ is close to $\{n^2\sqrt 2\}$ only if $\{(2n+1)\sqrt 2\}$ is close to $0$ or $1$. However $\{(2n+1)\sqrt 2\}$ lies in $[\frac{4}{10};\frac{6}{10}]$ infinitely often so $|\{(n+1)^2\sqrt2\}-\{n^2\sqrt2\}|\geq \frac{4}{10}$ infinitely often.

Note that this is not an if and only if situation, for example if you replace $n^2$ by $\sqrt n$ the $\limsup$ is still infinite even if $\{\sqrt{n+1}-\sqrt n\}$ will approach $0$ when $n\to \infty$. This is of course because $|\{\sqrt{n+1}\}-\{\sqrt n\}|$ is big when $\sqrt n < k < \sqrt{n+1}$ for some integer $k$, and that happens infinitely many times.

Note also that this doesn't use the equirepartition of $(n^2\sqrt2)_{n\in \mathbf N}$, it merely use the equirepartition of $((2n+1)\sqrt2)_{n\in \mathbf N}$.

Renart
  • 3,046
  • 1
    Hmm, since you're really working out things - what do the curly braces indicate? Indication that the enclosed expression is meant as elements of a sequence for increasing index? Or the "fractional part" function ? (but how can then in the OP's image the y-axis can exceed 1 and go up to millions?) Or both? Or ... ? – Gottfried Helms Oct 27 '16 at 11:56
  • 2
    ${x}$ is the fractionary part of the real $x$. I use parenthesis for sequences, and i edited my post so sequences are clearly recognisable. OP's image exceed $1$ because he's interested in $n|{(n+1)^2\sqrt2}-{n^2\sqrt2}|$, but it's sufficient to prove that $|{(n+1)^2\sqrt2}-{n^2\sqrt2}|\geq \varepsilon$ infinitely often for some $\varepsilon >0$. – Renart Oct 27 '16 at 12:30
  • 1
    Ahh, I was missing that, thank you very much. So things make sense to me now... – Gottfried Helms Oct 27 '16 at 13:12
  • Loosely related: if $|x_{n+1}-x_n| = o(n^{-1})$ the sequence can not be equidistributed. The $O(n^{-1})$ case is right on the border. If $x_n \asymp \log n$ then it is not equidistributed mod 1; there is no limit distribution - even though the difference is $|x_{n+1} - x_n| \asymp \frac{1}{N}$. – cactus314 Oct 29 '16 at 02:54
3

Let $x_n$ be a sequence and call $d_1(n)$ the number of times $\{x_k\}$ is in $I_1 = [0;\frac 14]$ when $k \in \{1 \ldots n\}$, and $d_2(n)$ the number of times they are in $I_2 = [\frac 12 ; \frac 34]$.

Let $\epsilon \in (0 ; \frac 18)$.

If $(x_n)$ is uniformly distributed mod $1$ then $d_1(n)/n$ and $d_2(n)/n$ converge to $\frac 14$ as $n$ gets larger, so there is an integer $m$ such that $|d_i(n)/n - \frac 14| < \epsilon$ for $n \ge m$.

Then, $d_i(m) < (\frac 14+\epsilon)m < d_i(\frac{1+4\epsilon}{1-4\epsilon}m)$.

and so there must be for both $i$ at least one index $n_i$ between $m$ and $m' =\frac{1+4\epsilon}{1-4\epsilon}m$ such that $\{x_{n_i}\} \in I_i$.

Then, letting $A = \max_{m < n \le m'} \{n|x_n-x_{n-1}|\}$, and supposing $n_1 < n_2$ for convenience,
$\frac 14 \le |x_{n_1} - x_{n_2}| \le A(\frac 1{n_1+1} + \ldots \frac 1{n_2}) \le A \log(\frac{n_2}{n_1}) \le A \log(\frac {m'}m) = A \log (\frac {1+4\epsilon}{1-4\epsilon}) \le 8A\epsilon\log 3$
(the last inequality comes from $\epsilon < \frac 18$ and a bit of analysis )

This proves that $A \ge C/\epsilon$, where $C = 1/(32\log 3) > 0$.

By taking smaller and smaller values for $\epsilon$ this shows that $(n|x_n-x_{n-1}|)$ must have larger and larger values, and so it must be unbounded.

mercio
  • 51,119
  • Are you trying to prove the theorem in general? I am going around and around your argument. You sure $\frac{1+x}{1-x} \leq 3^{2x} $ ? This is like saying $1+2x \leq e^{2x} $ (meaning you can do slightly better than $\log 3$). I have to keep reading. – cactus314 Oct 29 '16 at 01:31
  • yeah I'm proving that if the sequence is uniformly distributed then $n(x_n-x_{n-1})$ is unbounded (which is equivalent to $n(x_{n+1}-x_n)$ is unbounded). The inequality is true for $0 \le x \le 1/2$, and of course you can always do better if you restrict $x$ to be closer to $0$. I just wanted to have something simpler than the log thing to get a clearer picture. That step is not really necessary – mercio Oct 30 '16 at 09:55
  • after some scratch-work, the worst case is when $x_n - x_{n-1}$ and $\frac{1}{n}$ are at the same scale: $x_n - x_{n-1} \asymp \frac{1}{n}$. – cactus314 Oct 30 '16 at 22:20