11

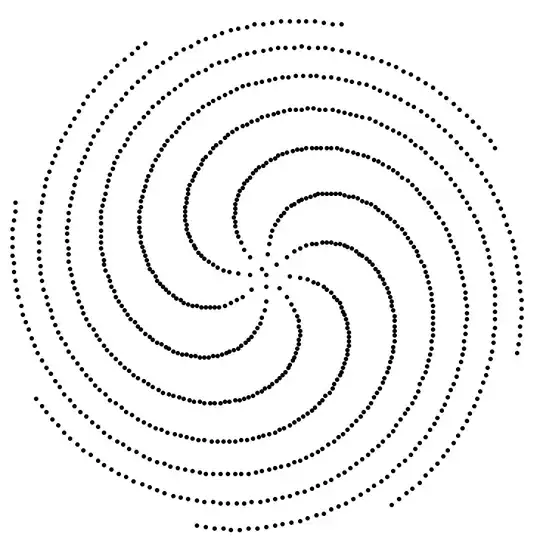
Vogel's model for sunflower seed arrangement uses discrete points on a spiral, with a very specific turning angle of $\theta_1 = 2\pi/\phi^2$ where $\phi = \frac{1+\sqrt{5}}{2}$ is the golden ratio: $$ \theta_k = \frac{2\pi}{\phi^2} k, \qquad r_k = c\sqrt{k}, \qquad k=0,1,2,\dots $$

This produces an arrangement like this: Points on a Fibonacci spiral

The points appear to have approximately the same distance from their neighbours. We perceive a nice even distribution.

Modifying the turning angle even slightly destroys this nice property. Example (angle changed by 2%):

Points on a nearly-Fibonacci spiral Points on a nearly-Fibonacci spiral

I am looking for insight (if not an exact derivation) into why this angle is so special, and what other angles will work. What property of the angle causes the points to be approximately equidistant?

By experimentation, $2\pi/\phi$ also works, and so does $2\pi/(\phi + \text{integer})$. But most other numbers, such as $2\pi/\phi^3$, don't.

I found many web pages that show this spiral, but they don't explain how this property arises, or how one might derive angles that have this property. I am surprised by that because I expected that there would be a simple explanation.

This point arrangement in also used in numerical methods that require distributing points on the sphere evenly: https://stackoverflow.com/a/26127012

Community
  • 1
Spiros
  • 111
  • Link for second image: two Insufficient reputation to post it directly. – Spiros Sep 20 '16 at 11:24
  • I edited to add your image. – E. Joseph Sep 20 '16 at 12:01
  • 1
    You can read the author's article about this, there's a chapter which explains why is the angle 137 deg. Here is the link: link – 9cvele3 Sep 20 '16 at 12:07
  • 1
    Let me recommend https://www.youtube.com/watch?v=ahXIMUkSXX0 and its two sequels – Ben Millwood Sep 20 '16 at 12:12
  • @BenMillwood Nice video but the pace literally makes me dizzy for some reason ... Cvele: will read, thanks. – Spiros Sep 20 '16 at 12:16
  • That's a great reference by Cvele! The minimal distance part in Vogel's paper was a bit hard to follow, though. @Spiros: regarding $\phi^{-2},\phi^{-1},\phi$ and $\phi^2$ as well as $1/(\phi+n)$ for $n=-2,-1,1$ and $1/(\phi^2-1)$ working equally well, all those can be written in the form $\pm\phi+n$ for some integer $n$ so they all essentially provide the same angles. This can be verified applying $\phi^{m}=\phi^{m-1}+\phi^{m-2}$ in different ways. – String Sep 23 '16 at 09:37

1 Answers1

2

The problem with Vogel's model is that it obscures the structure of curves from which the points are derived. If you plotted it as a line instead of points it would look like a spirolateral with lines crisscrossing all over the place. In fact, as revealed by your modified drawings, it's really four evenly spaces Fermat spirals. The Fermat spiral is given by

$$ r(\theta)=\sqrt{\theta}\\ \theta\in[0,n\pi] $$

where $n$ is the number of half-turns.

To complete the the pattern, you need to concatenate the above with its anti-symmetric twin and then repeat for the number of arms desired by rotating the (dual) Fermat spiral by $\pi/\text{arms}$ for however many arms there are. Alternatively, you could take the (half) Fermat spiral and rotate it by $2\times\text{arms}$.

When programming the above you have several parameters at your disposal. Here is a pseudocode for how I do this in the complex plane

theta=0,n*pi,npts
r=sqrt(theta)
z=r*exp(i*rho*theta)
z=[-z;z]  % complete the spiral
for k=2:arms
    z=[z z*exp(i*k*pi/arms)]
end
plot(z) % using lines or dots

So the parameters are (1) the number of half turns, n, (2) the number of points on the curve, npts, (3) a stretching or density factor, rho, and (4) the number of arms. Using 2 (half) turns, 4 arms, 41 points, and a density of 1.4 I close to Vogel's pattern, but I haven't tried to fine tune it. I have not tried to incorporate $\varphi$ into the selection of the parameters.

Cye Waldman
  • 8,196