I got a problem which is to show that the circle that is the intersection of the plane $x+y+z=0 $ and the sphere $x^2+y^2+z^2=1$ can be expressed as $$x(t)=\frac{\cos(t)-\sqrt{3}\sin(t)}{\sqrt{6}},$$ $$y(t)=\frac{\cos(t)+\sqrt{3}\sin(t)}{\sqrt{6}}$$ and $$z(t)= \frac{-2\cos(t)}{\sqrt{6}}.$$ The circle turns out like a $45$ degree circle in three dimensions. I know if the circle is in two dimensions like $x$ and $y$, the parametrization will be $(x(t),y(t))=(r\cos(t),r\sin(t))$. But in this question , what should I do?
Asked
Active
Viewed 2,203 times
2
-
1you will need the middlepoint of the sphere and the equation of the line that goes through the middlepoint of the sphere and is perpendicular to the plane – Dr. Sonnhard Graubner Sep 17 '16 at 12:42
-
Related: Determine Circle of Intersection of Plane and Sphere. Here, writing your parametrization in the form $\cos(t) \mathbf{u}{1} + \sin(t) \mathbf{u}{2}$ should help, the point being that $(\mathbf{u}{j}){j=1}^{2}$ is an orthonormal basis of your plane. – Andrew D. Hwang Sep 17 '16 at 13:23
1 Answers
-1
Here is how I solved for the intersection of the plane $x+y+z=1$ and the sphere $x^2+y^2+z^2 = 1$, which is a little different with your question but the steps are typically the same.
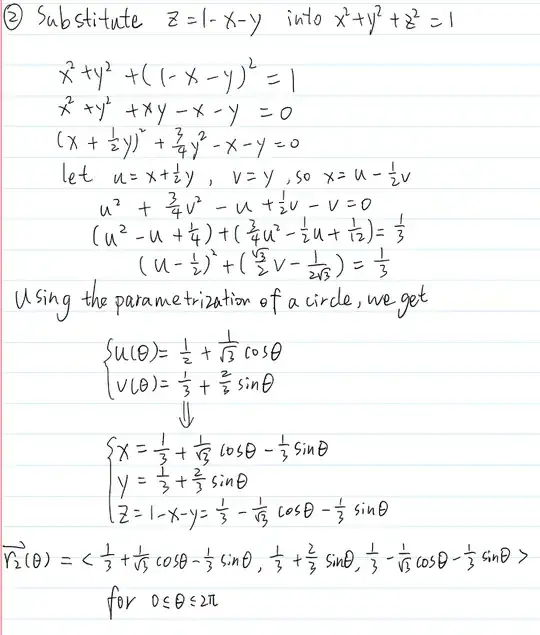
Siong Thye Goh
- 153,832