1

I was solving a uniform probability distribution question, the question was : $\\$ probability of meeting two people A and B between 1 PM and 2 PM, if none of them waits more than 15 minutes for the other. Given that probability of arrival is uniform between 1 PM to 2 PM for both of them.

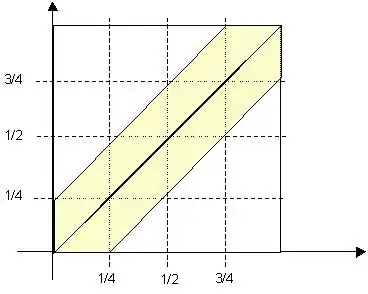
I took the time span as L and separated two zones. [0,3L/4] and [3L/4,L].

In the first zone if A comes first at time x B has the option to come anytime in [x,x+L/4]. In the second zone,if A comes first at x then B must come in [x,L-x].

I did the integration in two zones and found P(A-B) = 7/32,and multiplied by 2 gives the total probability.

Later I framed (visualized) the same question as follows : In Cartesian co-ordinate system,along the x axis two points p and q are selected uniformly at random in $\left [ 0,L \right ]$ where L > 0.What is the probability of $\text{dist(p,q)} \leq \frac{L}{4}$.

Then I modified it to two dimensional geometry problem :

In the Cartesian plane, selection of a point P along the y axis in [0,2] is uniformly random. Similarly selection of a point Q along the x axis in [0,2] also uniformly distributed. What is the probability of the area of the triangle POQ to be less than or equal to 1, where O is the origin ?

I solved it using integration in two parts:

  • if x is in [0,1] then y is allowed to have the full range of [0,2]
  • if x is in [1,2] then y is allowed to have the range [0,2/x]

I got probability as 0.846.

My questions are:

  • Is it correct ?
  • What is the more generic way to to such problem ? In both the above cases I drew some geometry and did some integration. In the second problem, we are interested in the quantity area (xy/2). But what if we are given a random expression like (3xy+x^2). Please elaborate any other method.
Debashish
  • 885

2 Answers2

1

Your description is very hard to follow, but I think it looks correct.

By integration did you do?: $$\begin{align}P ~=~& \int_1^2\int_{\max(1,a-1/4)}^{\min(2,a+1/4)} f_{\scriptsize A,B}(a,b) \operatorname d b\operatorname d a \\[1ex] =~& \int_1^{1+1/4}\int_{1}^{a+1/4} 1 \operatorname d b\operatorname d a+\int_{1+1/4}^{2-1/4}\int_{a-1/4}^{a+1/4} 1 \operatorname d b\operatorname d a+\int_{2-1/4}^2\int_{a-1/4}^{2} 1 \operatorname d b\operatorname d a \end{align}$$

Or via complements: $$\begin{align}P ~=~& 1-\int_1^{2-1/4}\int_{a+1/4}^2f_{\scriptsize A,B}(a,b) \operatorname d b\operatorname d a-\int_{1+1/4}^2\int_1^{a-1/4}f_{\scriptsize A,B}(a,b) \operatorname d b\operatorname d a \end{align}$$

Geometrically:

Draw a square, $[1;2]^2$. On it mark lines $\overline{(0,\tfrac 14)(2-\tfrac 14,1)}$ and $\overline{(\tfrac 14,0)(1,2-\tfrac 14)}$. The proportionate area of the enscribed hexagon is the measure you seek.

$$P=(2-\tfrac 14)(\tfrac 14) = \tfrac 7{16}$$

In the second problem you do indeed seek $$\begin{align} \iint_{x\in(0;2),y\in(0;2),xy\leq 2} \tfrac 14\operatorname d(x,y) ~=~& \int_0^2\int_{0}^{\min(2,2/x)}\tfrac 14\operatorname d y\operatorname d x \\ =~& \int_0^1\int_0^2\tfrac 14\operatorname d y\operatorname d x+\int_1^2\int_0^{2/x}\tfrac 14\operatorname d y\operatorname d x\\~=~&\tfrac 12+\tfrac 12\ln 2 \\\approx~& 0.846573590279972654708616060729088284037750067180 \end{align}$$

Graham Kemp
  • 133,231
1

The event $x$ and $y$ are independent and uniformly distributed so that geometrically the event space is represented by a square $1\;h\; \times \,1\;h$ of uniform density. The condition for the meeting to take place is.

$$ \left| {y - x} \right| \leqslant 1/4 $$ i.e. $$ 0 \leqslant y - x \leqslant 1/4\quad \vee \quad - 1/4 \leqslant y - x < 0 $$ or $$ x \leqslant y \leqslant x + 1/4\quad \vee \quad x - 1/4 \leqslant y < x $$ which is the area in yellow in the sketch.
Pmeet

The probability of meeting is easily calculable as: $$ P_{\text{meet}} = 1 - 2\frac{1} {2}\left( {\frac{3} {4}} \right)^2 = \frac{7} {{16}} $$

G Cab
  • 35,964