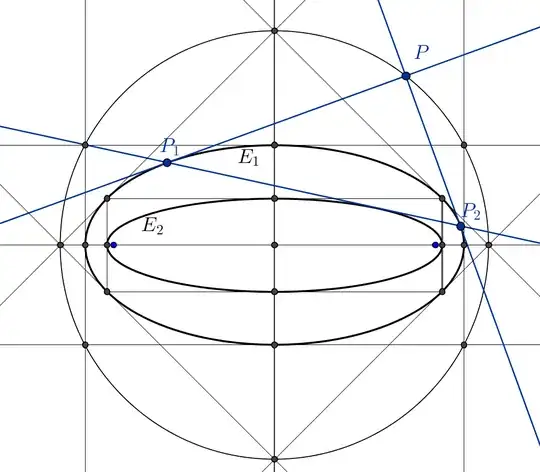
Suppose a tangent to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ cuts the ellipse $\frac{x^2}{c^2}+\frac{y^2}{d^2}=1$ at points $P,Q$, and that the tangents to the second ellipse at $P,Q$ are perpendicular. Determine $\frac{a^2}{c^2}+\frac{b^2}{d^2}.$
I tried as: I take a point on inner ellipse and from that wrote the equation of tangent and then tried to find the intersection points to other ellipse . But this became too complicated.
Can anyone please give me how to proceed?