8

spherical harmonics (below image)

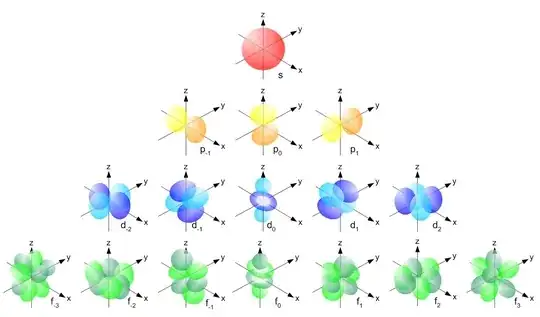
enter image description here

Schrödinger equation(below image)

enter image description here

What is the relationship between spherical harmonics and the schrodinger equation?

User3910
  • 2,440
  • 4
    Do you mean the other way around, how are spherical harmonics derived from Schrodinger ? – Rene Schipperus Sep 06 '16 at 15:22
  • @ReneSchipperus It appears so. – User3910 Sep 06 '16 at 16:16
  • http://physics.stackexchange.com/questions/278571/how-was-schr%C3%B6dingers-equation-derived-from-spherical-harmonics/278587#278587 – User3910 Sep 07 '16 at 15:33
  • 1
    Short answer: Spherical harmonics are (the angular part of) solutions to a certain class of differential equations. With a central potential, Schroedinger's equation falls into that class. In particular, the classical (i.e., quantum mechanical and non-relativistic) hydrogen atom has a radial potential $V(r) = 1/r$, so the spherical harmonics appear as electron shells. – anomaly Sep 07 '16 at 16:07

2 Answers2

6

Quite the opposite: Spherical harmonics are found to be eigenfunctions for the angular momentum operator $L^2$, which all comes from the Schrödinger equation (SE). If you want to see how to get from SE to the spherical harmonics, I suggest you pick up an introductory text on Quantum Mechanics - it is far too big an endeavor to undertake here.

Edit to answer OPs edit:

SE (in the eigenbasis) is $$\hat{H}\psi=E\psi,$$ where $\hat{H}$ is the Hamiltonian. The Hamiltonian is an operator (which is not a number, but more like a matrix... that is the reason for the "hat") that basically specifies what system you're looking at. A lot of problems in QM goes like "write down $\hat{H}$ for the system at hand, then solve SE."

Now, $\hat{H}$ is special because the eigenvalues associated with it are the allowed energy states for the system, which determines how it behaves. As you may know, the energy of a system can be split up into the kinetic energy $\hat{T}$ and the potential energy $\hat{V}$. We can therefore write $\hat{H}=\hat{T}+\hat{V}$. Here's the connection with the spherical harmonics: Whenever $\hat{V}$ is spherically symmetric (and SE is separable), the eigenfunctions $\psi$ of $\hat{H}$ will have a polar part. This polar part is precisely the spherical harmonics. This is for instance the case in the famous example of the hydrogen atom.

Bobson Dugnutt
  • 10,912
  • Would it be possible to think in octahedral values? Spherical harmonics related to Cartesian coordinates. But the Nobel gases Ne and Ar have 8 electrons in the outer shell and a octahedron system matches it much better. To illustrate what I mean see my elaboration about the Distribution of magnetic dipole moments in atoms. – HolgerFiedler Sep 06 '16 at 19:03
  • Be very careful when saying that an operator is "more like a matrix" in QM, as it the standard example of operators not having a matrix representation (see $x$ and $p$, for example). – gented Sep 07 '16 at 00:10
  • @GennaroTedesco I would say thinking about operators as matrices is pretty fruitful: In the case that your Hilbert space is finite dimensional, they are matrices, and in the infinite dimensional case (for example $x$ and $p$) the operators can be thought of as being infinite dimensional matrices. Of course "linear transformation" is the correct term here, but explaining what that means would be far more arduous (and possibly confusing), so I went for "more like matrices than numbers" as OP is more likely to know what a matrix is and this still offers a way of thinking about operators. – Bobson Dugnutt Sep 07 '16 at 05:08
6

The Schrödinger equation, and in particular the Schrödinger equation with $1/r$ electric potential function, is not something that you can "derive" from mathematics. Mathematically it would be perfectly consistent for photons to be massive (which would result in a Yukawa potential rather than $1/r$).

Robert Israel
  • 470,583
  • 4
    $1/r$ doesn't have anything to do with spherical harmonics. These spherical functions are eigenfunctions of any spherically-symmetric Hamiltonian, e.g. 3D harmonic oscillator. Yukawa potential would also give spherical harmonics as eigenfunctions. – Ruslan Sep 06 '16 at 15:43
  • 3
    @Ruslan that's exactly the point, is it not? The spherical harmonics tells you nothing about the "radial" part of the dynamics, and so you cannot "derive" the Schrodinger equation from it (since Yukawa potential, for example, also is compatible with the harmonics). – Willie Wong Sep 06 '16 at 18:35