What does the second antiderivative of a function represent?

Question

If the antiderivative represents the area under the curve from $f(0)$ to $f(x)$ what does the second antiderivative or the antiderivative of the antiderivative represent?

Sarcastically speaking the area under the curve of the anti derivative, but great question. — Sigma6RPU, Aug 27 '16 at 22:21
@Sigma6RPU wow thank you I'm really not sure why it was so hard to wrap my head around that — AJB_1070179, Aug 27 '16 at 22:35
I was joking of course, and being serious. But for real great question. — Sigma6RPU, Aug 27 '16 at 22:38
$\int_0^xf(t),dt$ is the area under the curve from $0$ to $x.$ — zhw., Aug 27 '16 at 22:53
Assuming you have some initial conditions and if $f$ represents the acceleration of a particular over time, then the second antiderivative will give you the position of the particle over time. You can extend this idea to the "acceleration" of any quantity with respect to time or any other quantity. — benguin, Aug 27 '16 at 23:23
The second integral could be thought about the same way in terms of physical changing quantities. Basically you are asking what the position function means in retrospect to acceleration. — Sigma6RPU, Aug 28 '16 at 01:02
But yes what I meant before is correct it is the area underneath the first integral. — Sigma6RPU, Aug 28 '16 at 01:03
You could also imagine the second antiderivative to represent "extruding" the area represented by the first antiderivative into a solid. — Anthony D'Arienzo, Aug 29 '16 at 02:30
Wikipedia suggests It should be “an” rather than “the antiderivative”, as there are many; $f(0)$ is not assumed as a string point — but maybe the usage varies. — PJTraill, Aug 31 '16 at 18:03

score 1 · Answer 1 · edited Apr 13 '17 at 12:21

Strictly speaking, the premise "If the antiderivative represents the area under the curve from $f(0)$ to $f(x)$" is iffy: A function $f$ having one antiderivative has infinitely many (as PJTaill says), so one can't speak of the antiderivative. (If the domain is an interval, any two antiderivatives differ by a constant. If the domain is disconnected, there can be "independent constants in each component.")

Second, "the area under the curve from $f(0)$ to $f(x)$" presumably refers (as zhw notes) to the portion of the fundamental theorem of calculus guaranteeing that if $f$ is continuous on an interval containing $0$ and $x$, the function $$ F_{1}(x) = \int_{0}^{x} f(t)\, dt $$ is an antiderivative of $f$. The identification of $F_{1}(x)$ with a certain area is arguably more of an interpretation than an identification, however. (Separately, as a fine point, if $f$ has a jump discontinuity at $x$, the function $F_{1}$ is not an antiderivative of $f$ at $x$, and in fact no function is an antiderivative of $f$ at $x$. This is not a trivial nitpick: An integrable function can have a jump discontinuity at each rational number, for example.)

The comments of Sigma6RPU and Anthony D'Arienzo note that the second antiderivative may similarly be interpreted as the volume of the solid obtained by extruding the area under the graph $y = f(x)$. Analytically, put $$ F_{2}(x) = \int_{0}^{x} F_{1}(s)\, ds = \int_{0}^{x} \int_{0}^{s} f(t)\, dt\, ds = \int_{0}^{x} \int_{t}^{x} f(t)\, ds\, dt = \int_{0}^{x} (x - t) f(t)\, dt. $$

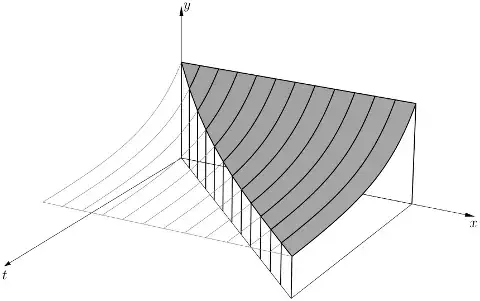
In case it's of interest, the preceding iterated formula generalizes (compare with the integral form of the remainder in Taylor's theorem) to $$ F_{n}(x) = \frac{1}{(n - 1)!} \int_{0}^{x} (x - t)^{n-1} f(t)\, dt, $$ whose $n$th derivative is easily checked to be $f$, provided $f$ is continuous. The value $F_{n}(x)$ can be interpreted geometrically as an $(n + 1)$-dimensional volume obtained by "successive extrusion", but is probably best regarded analytically.

If you're seeking a physical interpretation along the lines of What does the integral of position with respect to time mean?, beware that the question is deeper than it naively appears.

What does the second antiderivative of a function represent?

1 Answers1