Finding a value on a number line?

Question

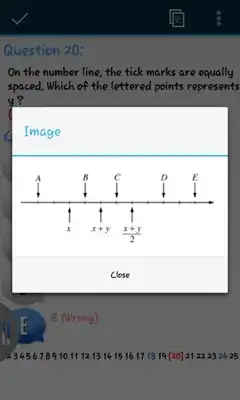
I came across this question: On the number line the tick marks are equally spaced which of the lettered points represent $y$

The solution says it is $D$ but I think it is $E$.

Explanation

The average $\frac{x+y}{2}$ shows it is the midpoint of $x$ and $y$ and thus counting the steps we get $E$
I can see that $\frac{y}{2}$ is the partition. Also that $x$, $x+y$ and $\frac{x+y}{2}$ are all negative and $\frac{y}{2}$ is positive because the points are on a number line. My aim is finding the origin $0$. So I can count two partitions to get $y$. If I separate $\frac{x+y}{2}$ to $\frac{x}{2}+\frac{y}{2}$ I can see that $C$ is $\frac{x}{2}$ and that moving $3$ partitions from $C$ I get my origin which is on $D$. going two steps gets me to $E$. So what seems to be the problem?

I'm assuming it is a typo. Notice that the origin need to be D so perhaps the question is what point represents 0. — fleablood, Aug 27 '16 at 18:12
x + y - (x)= y =2. $(x+y)/2 - x = 4$ so $x/2 - x + 1 = 4$ so $x - 6$. So D = 0. and y= 2 = E. (Assuming the tick marks are = 1; if the tick marks are any k, we still get 0 = D, y = 2k=E, x = -6k. — fleablood, Aug 27 '16 at 18:17
It'd be good to get a third opinion to avoid dyslexia and brain farts but it sure seems like your reasoning it the correct one. — fleablood, Aug 27 '16 at 18:48
Despite the name, "linear algebra" is not an appropriate tag for this; I've retagged. — Noah Schweber, Aug 27 '16 at 19:12

user0 · Answer 1 · 2018-08-31T15:43:20.177

Answer -

Yes, you are correct, $y$ should be $E$.

Note that there are two spaces between $x$ and $x+y$, so $y=2$.
${(x+y) \over 2}$ is to the right of $(x+y)$, so , $(x+y)$ must be negative.
As, $y$ is positive from $(1)$, so $x$ must be negative from $(2)$.
Now, ${(x+y)\over 2}$ is halfway between $(x+y)$ and $0$. Also, counting the steps from $(x+y)$ to ${(x+y)\over 2}$ shows that ${(x+y)\over 2}=(-2)$.
From $(4)$, we can count $2$ steps to the right to see that $D$ is $0$ and so $y=2$ is $E$.