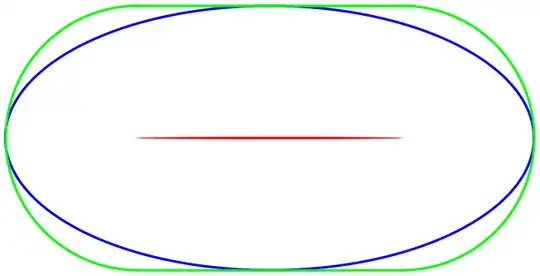
Given an ellipse, $E_1$ with radii $r_x, r_y$ I would like to know whether the minimum distance between any selected point, $P_a$, and $E_1$ is less than, say $D$.
I have seen the related question of finding the distance between a point and an ellipse. Rather than finding that minimum distance, I would like to solve it differently by creating an ellipse, $E_2$ with radii $r_x + D, r_y + D$ and then test whether the point $P_a$ falls within $E_2$, which is easy to do.
So, my question is, if the point $P_a$ falls within $E_2$, does it mean that the minimum distance between $E_1$ and $P_a$ is less than $D$?