There is a related discussion:
closed epigraphs equivalence
Showing that projections $\mathbb{R}^2 \to \mathbb{R}$ are not closed
My problem is rather simple:
A function is closed if its epigraph is closed.
For example:
- $f(x) = x^2$ (also a convex function with its epigraph convex.)
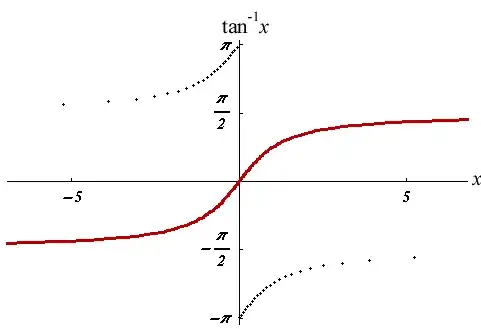
- $f(x) = \tan^{−1} (x)$
However, I am confused about like the first case, the epigraph approaches infinity as $y\rightarrow \infty$. The second case, the epigraph approaches infinity as $x\rightarrow\infty$. The epigraph has no boundary on the right and left directions.
I cannot understand why their epigraph is closed.