11

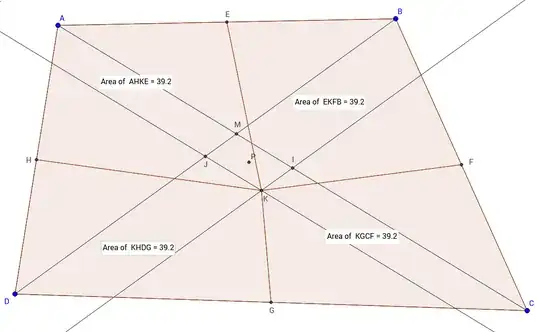
Consider an irregular quadrilateral $ABCD$. Let $E,F,G,H$ be the midpoints of its edges. It seems that there is a point $K$ such that $$ S_{AHKE} = S_{EKFB} = S_{KHDG} = S_{KGCF} \left(= \frac{1}{4} S_{ABCD}\right) $$ I'm curious whether the point $K$ has any other interesting properties. enter image description here

Here's the proof that this point does exist: Assuming that $A,B,C,D,I$ have coordinates $\mathbf p_1, \mathbf p_2, \mathbf p_3, \mathbf p_4, \mathbf p$, respectively. Then $$ \mathbf S_{AHKE} = \frac{1}{2} (\mathbf p - \mathbf p_1) \times \frac{\mathbf p_2 - \mathbf p_4}{2} = \frac{1}{4} (\mathbf p - \mathbf p_1) \times (\mathbf p_2 - \mathbf p_4)\\ \mathbf S_{EKFB} = \frac{1}{4} (\mathbf p_3 - \mathbf p_1) \times (\mathbf p_2 - \mathbf p) = \frac{1}{4} (\mathbf p - \mathbf p_2) \times (\mathbf p_3 - \mathbf p_1)\\ \mathbf S_{KHDG} = \frac{1}{4} (\mathbf p_3 - \mathbf p_1) \times (\mathbf p - \mathbf p_4) = \frac{1}{4} (\mathbf p_4 - \mathbf p) \times (\mathbf p_3 - \mathbf p_1)\\ \mathbf S_{KGCF} = \frac{1}{4} (\mathbf p_3 - \mathbf p) \times (\mathbf p_2 - \mathbf p_4) $$ It is easy to see that $$ \mathbf S_{AHKE} + \mathbf S_{KGCF} = \frac{1}{2} \mathbf S_{ABCD}\\ \mathbf S_{EKFB} + \mathbf S_{KHDG} = \frac{1}{2} \mathbf S_{ABCD} $$ thus there is exactly two linear equations $$ \mathbf S_{AHKE} - \mathbf S_{KGCF} = 0\\ \mathbf S_{EKFB} - \mathbf S_{KHDG} = 0 $$ to determine two components of $\mathbf p$. And they are $$ (2\mathbf p - \mathbf p_1 - \mathbf p_3) \times (\mathbf p_2 - \mathbf p_4) = 0\\ (2\mathbf p - \mathbf p_2 - \mathbf p_4) \times (\mathbf p_3 - \mathbf p_1) = 0 $$ which is equivalent to $$ \mathbf p = \frac{\mathbf p_1 + \mathbf p_3}{2} + \lambda(\mathbf p_2 - \mathbf p_4) = \frac{\mathbf p_2 + \mathbf p_4}{2} + \mu(\mathbf p_3 - \mathbf p_1), \quad \lambda,\mu \in \mathbb R $$ The geometrical definition of $K$ should be obvious now: the point $K$ is reflection of diagonal intersection point $M = AC \cap BD$ about the vertices' centroid $P$

uranix
  • 7,773
  • 1
  • 22
  • 57
  • 1
    Nice catch. I guess that your geometric description of $K$ also follows from the fact that the area of the Varignon parallelogram $EFGH$ is half the area of $ABCD$. – Jack D'Aurizio Aug 11 '16 at 14:15
  • 2
    A little remark ; One should be cautious about centroids : you should say it is the "vertices' centroid". Because the area centroid is in general different (and the sides' centroid is a third point...). We are usually abused by the fact that in a triangle, vertices' centroid and area centroid always are the same. – Jean Marie Aug 12 '16 at 21:46
  • 1
    A historical note: This result was published in Crelles Journal in 1841 by Brune (see: https://de.wikipedia.org/wiki/Satz_von_Brune) – Anton Steinfadt Feb 13 '24 at 20:24

1 Answers1

2

From your definition of $K$ it follows that triangles $EBK$ and $GCK$ have the same area, which is the same as saying that triangles $ABK$ and $DCK$ have the same area. In other words: $K$ divides $ABCD$ into two couples of triangles of equal area.

Given two segments $AB$ and $CD$ whose extensions meet at $Q$ (see picture below), the locus of points $X$ such that $XAB$ and $XCD$ have the same area, with $X$ belonging to $\angle AQD$, is line $QR$, where $R$ is the vertex opposite to $Q$ of the parallelogram with sides parallel and congruent to $AB$ and $CD$. A different but obvious construction is needed if $AB$ and $CD$ are parallel.

enter image description here

In the same way one can construct line $ST$, which is the locus of the points forming with $AD$ and $BC$ triangles of equal area. Point $K$ is then the intersection of $QR$ and $ST$.

Intelligenti pauca
  • 55,765