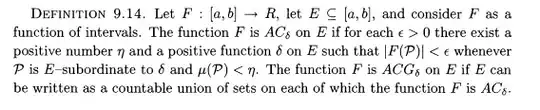I'd like to see a proof (or hints and outlines) for the following lemma, which is very useful to prove some interesting properties, including an Integration by Parts theorem for Henstock-Stieltjes integrals:
Let $f$, $g$ and $\varphi$ be (normally real) functions defined on $[a,b]$ and $f$ is $\varphi$-Henstock-Stieltjes integrable with $F(x)=\int_a^x f d\varphi$. Then $fg$ is $\varphi$-Henstock-Stieltjes integrable if and only if $g$ is $F$-Henstock-Stieltjes integrable and so we have $$\int_a^b fg d \varphi =\int_a^b g d F.$$
I think I'm able to show a simple version of this lemma where $\varphi(t)=t$ following the proof of 9.17 (image) given in The Integrals of Lebesgue, Denjoy, Perron and Henstock by Gordon A Russel, which is even more simple: he also takes $g(t)=1$. I'd like to know if it's possible to adapt this proof for what I want, or if I have to start from scratch.
This definition may be required: