6

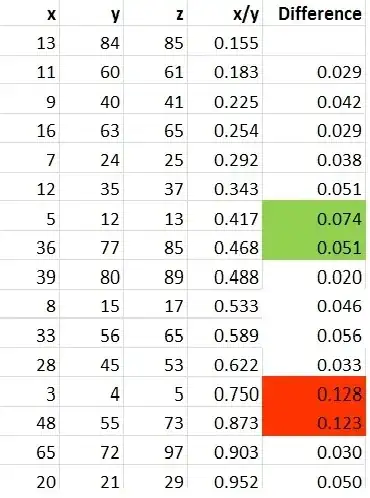
The table below lists the primitive Pythagorean triples $x^2+y^2=z^2$ with $z<100$ in ascending order of the ratio $x/y$. The final column shows the difference between each ratio and the preceding ratio in the list.

It can be seen that the differences in ratio (highlighted in red) before and after the smallest triple (3,4,5) are much larger than any other in the list. The differences (in green) before and after the next smallest triple (5,12,13) are also relatively large.

Question: Why are there no other small primitive Pythagorean triples close (in terms of the ratio) to (3,4,5)? Or is this just coincidence?

Given the general formula for Pythagorean triples $(m^2-n^2,2mn,m^2+n^2)$, the question seems to amount to showing that the ratio:

$$R=\frac{m^2-n^2}{2mn}$$

cannot be close to either $3/4$ or $4/3$ unless $m^2+n^2$ is fairly large. But I can't see how to proceed, other than by a case-by-case examination which would be equivalent to listing triples.

Pyth triples order by ratio

Adam Bailey
  • 4,735
  • 3
    Is this related to the fact that a rational number with a small denominator does not have other rational numbers with small denominators near it? If I remember right, two nonequal rational numbers $a/b$ and $c/d$ can't be closer together than $1/bd$. – Sophie Swett Jul 06 '16 at 12:08
  • @TannerSwett Yes, I suspect that is relevant. – Adam Bailey Jul 06 '16 at 12:21
  • This covers that: https://math.stackexchange.com/questions/7143/ – JCCyC Jul 09 '21 at 21:36

1 Answers1

4

Note that $\frac{3}{4}=\frac{r^2-1}{2r}$ has a solution $r=2$. Let now $r:=2+d$ for some rational number $d$, so that $$\delta:=\frac{r^2-1}{2r}-\frac{3}{4}=\frac{3+4d+d^2}{4+2d}-\frac{3}{4}=\frac{d(5+2d)}{4(2+d)}\,.$$ If you want $|\delta|\leq\frac{1}{20}$, then $$-0.07935<d<0.08062\,.$$ Every nonzero rational number $d$ within that range has denominator at least $13$. If $d=\frac{p}{q}$ with $q\geq 13$, then $$z\geq \frac{p^2+4pq+5q^2}{2}>\frac{q(q+4p)}{2}+2q^2> 2q^2 \geq 2\cdot 13^2=338>100\,,$$ as $|d|<\frac{1}{4}$ (making $q+4p>0$). The smallest $z$ that satisfies $|\delta|<\frac{1}{20}$ is $z=397$, i.e., for $(x,y,z)=(228,325,397)$, where $$\frac{3}{4}-\frac{x}{y}\approx 0.75- 0.701538 \lesssim 0.048462<\frac{1}{20}\,.$$

In fact, for any rational number $u$ and $\epsilon>0$, there exists $r\in\mathbb{Q}$ such that $$0<\left|\frac{r^2-1}{2r}-u\right|<\epsilon\,.$$ Take $u:=\dfrac{3}{4}$ and $\epsilon=\dfrac{1}{50000}$, then $r=\dfrac{100001}{50000}$ is a solution. Then, let $x,y\in\mathbb{N}$ be such that $\dfrac{x}{y}=\dfrac{r^2-1}{2r}$, and you will get a Pythagorean triplet $$(x,y,z)=\left(7500200001,10000100000,12500200001\right)\,,$$ with $$\frac{x}{y}=\frac{7500200001}{10000100000}\approx 0.750012$$ so that $$0<\left|\frac{x}{y}-u\right|<\epsilon\,.$$

Batominovski
  • 50,341