Given a great circle connecting two points on a sphere, what is the function describing it's equirectangular projection? In other words, given two longitudes and latitudes $(\phi_1, \theta_1)$ and $(\phi_2, \theta_2)$, what is the function $\theta(\phi)$ that describes a great circle passing between those points?
Attached is an image of exactly such function, representing flight routes, from the OpenFlights website.
$\quad\quad\quad$
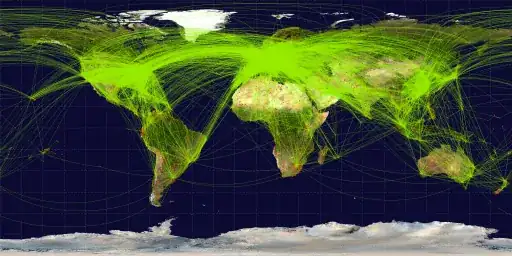
For the sake of simplicity, assume the Earth to be a perfect sphere.
First, any great circle is simply a plane passing through the origin. Second, we transform this to cylindrical coordinates to get the functional form. $$\alpha x + \beta y + \gamma z = 0$$ $$x^2 + y^2 + z^2 = 1$$ $$\sqrt{1-z^2}(\alpha \cos \phi + \beta \sin \phi) + \gamma z = 0$$ Merge into a single $\sin$ function: $$\alpha \cos \phi + \beta \sin \phi \to \alpha' \sin (\phi + \phi_0)$$ Leading to the general form:
$$z = \frac{ \sin (\phi + \phi_0)}{\sqrt{\delta^2 + \sin^2 (\phi + \phi_0)}}$$
Note that this function converges to a a sign function or zero in the limits $\delta\to 0, \delta\to \infty$ as required. Sample paths are shown below:
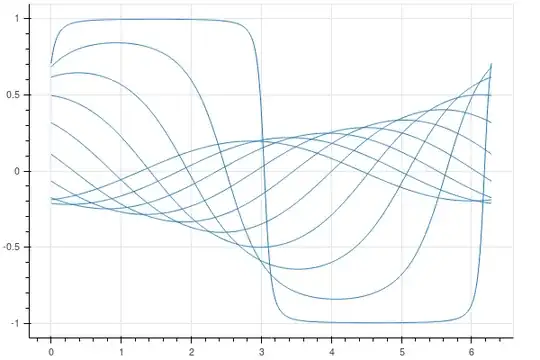
Thus to find the path between two arbitrary points $(\phi_1,z_1)$ and $(\phi_2,z_2)$ we can solve for $\delta$ and $\phi_0$, and use the above function for $z$. Extraction of $\delta$ leads to:
$$\delta^2 = \frac{1-z_1^2}{z_1^2}\sin^2 (\phi_1 + \phi_0)$$ $$\frac{z_1}{z_2}\sqrt{\frac{1-z_2^2}{1-z_1^2}}\sin (\phi_2 + \phi_0) = \sin (\phi_1 + \phi_0)$$ Denote: $$c\equiv \frac{z_1}{z_2}\sqrt{\frac{1-z_2^2}{1-z_1^2}}$$ Then:
$$\phi_0 = \arccos\left(\frac{\cos \phi_1 - c \cos \phi_2}{1+c^2-2c\cos(\phi_2 - \phi_1)}\right)$$
The full solution can then be composed from the above.
