Let $P$ denote $(x,y,z)\in \mathbb R^3$, which satisfies the inequalities:
$$-2x+y+z\leq 4$$ $$x \geq 1$$ $$y\geq2$$ $$ z \geq 3 $$ $$x-2y+z \leq 1$$ $$ 2x+2y-z \leq 5$$
How do I find an interior point in $P$?
Is there a specific method, or should I just try some random combinations and then logically find an interior point?
I tried the graphical method:
(Large versions here and here)
The affine half spaces with plane orthogonal to the coordinate axes (bound by red planes) are towards the viewer.
The other three half spaces (bound by cyan planes) contain the origin.
The feasible region seems to be the tetraeder with vertices $$ A = (2,3,5) \\ B = (2,2,3) \\ C = (1,3,3) \\ D = (1,2,3) $$ I first intersected planes to get lines, and then lines to get points. E.g. $A$ is the intersection of the three cyan planes and $D$ the intersection of the three red planes.
Rewrite the system of linear inequalities in the following order
$$x - 2y + z \leq 1$$
$$2x + 2y - z \leq 5$$
$$-2x + y + z \leq 4$$
$$x \geq 1$$
$$y \geq 2$$
$$z \geq 3$$
Adding the first two inequalities, we get $3 x \leq 6$, or, $x \leq 2$. Adding the 2nd and 3rd inequalities, we get $3 y \leq 9$, or, $y \leq 3$. Hence, $x+y \leq 5$. Adding the 1st and 3rd inequalities, we get
$$2 z \leq 5 + (x+y) \leq 10$$
or, $z \leq 5$. Combining these results with the 4th, 5th and 6th inequalities, we get
$$1 \leq x \leq 2 \qquad \qquad \qquad 2 \leq y \leq 3 \qquad \qquad \qquad 3 \leq z \leq 5$$
Thus, the polyhedron defined by the inequalities should be a subset of $[1,2] \times [2,3] \times [3,5]$. Let $x = 1$ and $y = 2$. Then, the inequalities give us $z \in [3,4]$. We can choose $z=3$. Hence,
$$(x,y,z) = (1,2,3)$$
is one feasible point. It is not the only one, though. It is also on the boundary. If we want an interior point instead, then let $x = \frac{3}{2}$ and $y = \frac{5}{2}$. The inequalities give us $z \in [3,\frac{9}{2}]$. We choose $z = 4$. Hence,
$$(x,y,z) = \left(\frac{3}{2},\frac{5}{2},4\right)$$
is one interior feasible point.
Label the planes and their intersection points as follows
$\begin{array}{llllllll} &\Pi_1:&x=1 & A & B & C & & & W & X\\ &\Pi_2:&y=2 & A & B & & D & & W & & Y\\ &\Pi_3:&z=3 & A & & C & D & & & X & Y & Z\\ &\Pi_4:&-2x+y+z=4 & & B & C & & E & & & Y & Z\\ &\Pi_5:&x-2y+z=1 & & B & & D & E & & X & & Z\\ &\Pi_6:&2x+2y-z=5 & & & C & D & E & W\\ \end{array}$
where $A=(1,2,3),B=(1,2,4),C=(1,3,3),D=(2,2,3),E=(2,3,5)$ are points which also satisfy all the inequalities and $W=(1,2,1),X=(1,\frac{3}{2},3),Y=(\frac{1}{2},2,3),Z=(0,1,3)$ fail to satisfy all the inequalities.
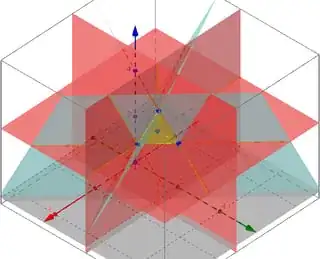
The five points $A,B,C,D,E$ are the vertices of a triangular bipyramid. The two pyramids are $ABCD$ and $BCDE$ with common base $BCD$ which is internal and not a face. The six faces are the planes $\Pi_i$.
The graphic below has the $z$-axis vertical, with $E$ the apex at the top ($z=5$), $B$ the vertex halfway down ($z=4$) and $\Pi_3=ACD$ the triangular base (at $z=3$). It has two hidden triangular faces - the base and the back $\Pi_6=CDE$. The light blue vertical face is $\Pi_1=ABC$, and the purple vertical face is $\Pi_2=ABD$. The other two visible faces are $\Pi_4,\Pi_5$.
The centroid of the polyhedron is $(1.4,2.4,3.6)$. It obviously satisfies the three inequalities related to $\Pi_1,\Pi_2,\Pi_3$. For $\Pi_4$ we have $-2.8+2.4+3.6=3.2<4$; for $\Pi_5$ we have $1.4-4.8+3.6=0.2<1$; and for $\Pi_6$ we have $2.8+4.8-3.6=4<5$.
You could also use the simplex method to solve the following problem: $$ \min\limits_{x,y,z,e,a}\quad Z= a_1+a_2+a_3 $$ subject to $$-2x+y+z+e_1 =4$$ $$x -e_2+a_1= 1$$ $$y-e_3+a_2=2$$ $$ z-e_4+a_3 = 3 $$ $$x-2y+z +e_5= 1$$ $$ 2x+2y-z +e_6= 5$$ $$ x,y,z,e,a\ge 0 $$
If $\min \{a_1+a_2+a_3\} = 0$, then you have a feasible point (with $a_1=a_2=a_3=0$).
Clever guessing is ok, random guessing isn't advised. Since $x\geq 1$, $y\geq 2$ and $z\geq 3$. You should try some values that are close to the boundary, since then they are less likely to break the other conditions. So an $x$ value slightly greater than $1$, a $y$ value that is slightly greater than $2$, and a $z$ value slightly greater than $3$.
So an interior point would be $(1.5, 2.5, 3.5)$ since
$$-2(1.5)+(2.5)+(3.5)=3< 4$$ $$1.5 > 1$$ $$2.5>2$$ $$ 3.5 > 3 $$ $$(1.5)-2(2.5)+(3.5)=0 < 1$$ $$ 2(1.5)+2(2.5)-(3.5)=4.5 < 5$$
