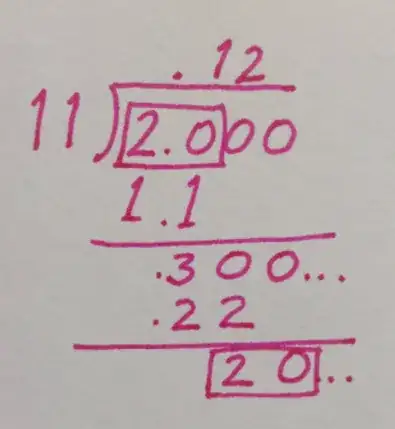Represent $\frac{2}{5}$ in quarternary form.

Question

I have the following intervals in Quaternary representation $$\bigg[0,\frac{1}{4}\bigg]=[0_4.0, 0_4.1]$$

$$\bigg[\frac{1}{4},\frac{2}{4} \bigg]=[0_4.1, 0_4.2$$

$$\bigg[\frac{2}{4}, \frac{3}{4} \bigg]=[0_4.2, 0_4.3]$$

$$\bigg[\frac{3}{4},1\bigg]=[0_4.3, 1_4.0]$$

I am trying to represent $\frac{2}{5}$ in quarternary form.

The working out gives the nested intervals

$[0,1], [0_4.1, 0_4.2],[0_4.12,0_4.13],[0_4.121.0_4.122]$

How do I get the solution $\frac{2}{5}=0_4.121212...$?

score 4 · Accepted Answer · edited Apr 13 '17 at 12:20

4

This answer will help you understand what I'm doing below.

We need to find: $$\frac 2 5=\frac{a}{4^b-1}$$ If we guess $b=1$, then we get a denominator of $3$, but then $a \notin \Bbb{Z}$, so that won't work. However, if we guess $b=2$, then we get a denominator of $15$ and $a=6$, so: $$\frac 2 5=\frac{6}{4^b-1}=\frac{12_4}{100_4-1}=0.\overline{12}_4$$

edited Apr 13 '17 at 12:20

Community

1

answered Jun 19 '16 at 21:52

Noble Mushtak

18,869

Why does $\frac{1}{8}=0_4.02$? – Al jabra Jun 20 '16 at 09:22
We know that $\frac 1 4=0.1_4$. Therefore, if we multiply both sides by themselves, we get $\frac{1}{16}=0.01_4$. Now, multiply both sides by $2$ to get $\frac 1 8=0.02_4$. – Noble Mushtak Jun 20 '16 at 11:26

score 1 · Answer 2 · answered Jun 19 '16 at 23:14

The answer of @NobleMushtak is perfect, but here’s another approach, which you can think of as experimental.

Take your $\frac25$, and multiply by $4$, and note the integer part. You’ve gotten $\frac85=1+\frac35$, so that the first base-$4$ digit is $1$. Now take your $\frac35$, and multiply by $4$ again to get $\frac{12}5=2+\frac25$. So the second base-$4$ digit is $2$, and you’re back to where you started. You may now guess that the base-$4$ expansion of $\frac25$ is $.121212\dots$, repeating, but you’d better check. That repeating representation denotes a convergent geometric series, $\frac6{16}+\frac6{16^2}+\frac6{16^3}+\cdots$, which your formula from high school $a/(1-r)$ tells you ($a=\frac6{16}$, $r=\frac1{16}\,$) works out to $$ \frac{6/16}{15/16}=6/15=2/5\,. $$

You may use exactly the same technique of multiplying repeatedlly by $4$ and looking at the integer part to find the base-$4$ expansion of $\pi$, for instance, out to (roughly) $\log10/\log4$ times as many base-$4$ digits as you had of decimal digits.

score 1 · Answer 3 · answered Jun 19 '16 at 23:25

1

You can also find the answer using long division (base $4$). After finding the first two places, $.12$, the remainder is $20\dots$, which was the starting point, so the answer is $.\overline{12}$.

answered Jun 19 '16 at 23:25

Steve Kass

15,314

Represent $\frac{2}{5}$ in quarternary form.

3 Answers3