A simple function $h$ (or random staircase function) is defined as
$$ h(t) = \sum_0^{n} \xi_i I_{(t_i,t_{i+1}]}(t) $$
where $0<t_1< \ldots < t_{n+1}<T$ and the $\xi_i$ are random variables.
Now the stochastic integral of the simple function $h$ is
$$\int_0^Th(t) dW_t := \sum_0^n\xi_i (W_{t_{i+1}} - W_{t_i})$$.
Questions:
- For the classic rieman integral each summand has constant width $\Delta x$ in the picture:
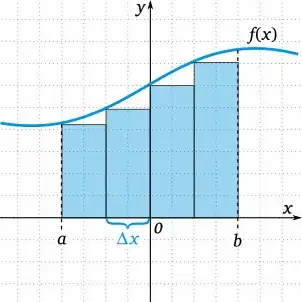
Can I think of the term $(W_{t_{i+1}} - W_{t_i})$ as beeing the same as the $\Delta x$, but different for each interval $(t_i, t_{i+1}]$ since Brownian Motion does not move a unit-speed like the variable x does?
Edit: One of the questions has an answer here.
- The stochastic integral results in a new random process, but the sum combines all the random variables. Why isn't the result a single random value?
Edit2: removed stupid second question.