1

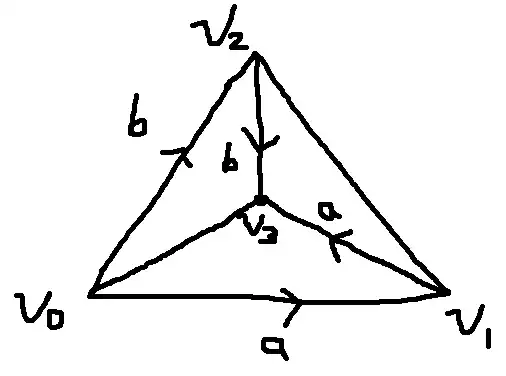
I have been stuck on this question for a long time:

Show that the $\Delta$-complex obtained from $\Delta^3$ by performing the edge identifications $[v_0,v_1]\sim [v_1,v_3]$ and $[v_0,v_2]\sim [v_2,v_3]$ deformation retracts onto a Klein bottle.

What I tried: I am aware that the way to do this type of question is by repeated cutting and gluing, until the diagram resembles the fundamental polygon of the Klein bottle. Unfortunately, I am not sure how to go about this.

I drew a basic picture of $\Delta^3$ as such. How do I go about making the first cut to identify $[v_0,v_1]\sim [v_1,v_3]$?

enter image description here

P.S.: I am aware of this question (Show that the $\Delta$-complex obtained from $\Delta^3$ by performing edge identifications deformation retracts onto a Klein bottle.), but I don't really understand his solution, besides in the comments someone said it is wrong.

Thanks for any help. I am looking for the simplest possible proof, if possible just using diagrams of "cutting and gluing", a proof-without-words of sorts. Not sure if such a proof is possible though.

Community
  • 1
yoyostein
  • 20,428

1 Answers1

1

Consider, in the 1-skeleton of the tetrahedron $T$, the closed edge path $$b = [v_0,v_1] * [v_1,v_3] * [v_3,v_2] * [v_2,v_0] $$ You can turn $T$ so that its projection onto the plane is a square, such that $b$ projects to the boundary of that square.

The square can in turn be embedded into $T$, forming a kind of distorted square $Q \subset T$, so that the boundary of $Q$ is $b$. One way to understand this embedding is that there is a homeomorphism between $T$ and the 3-ball taking $b$ to the equator, and under this homeomorphism $Q$ corresponds to the 2-disc bounded by the equator and cutting the 3-ball into two equal halves.

There is also a deformation retraction $f : T \to Q$. Under the homeomorphism described above this corresponds to a deformation retraction from the 3-ball to the 2-disc.

Now glue the edges, by an equivalence relation that I'll denote $\sim$, forming a quotient map that I'll denote $T \mapsto T/\!\sim$. Since the four edges that are glued form the four sides $b$ of the distorted square $Q$, we also obtain a quotient map $Q \mapsto Q / \!\sim$, and evidently $Q/\!\sim$ is homeomorphic to the Klein bottle.

Finally, the deformation retraction $f : T \to Q$ descends to a deformation retraction $$F=f/\!\sim \,\, : \,\, T/\!\sim \,\, \to \,\, Q/\!\sim $$

Lee Mosher
  • 135,265