6

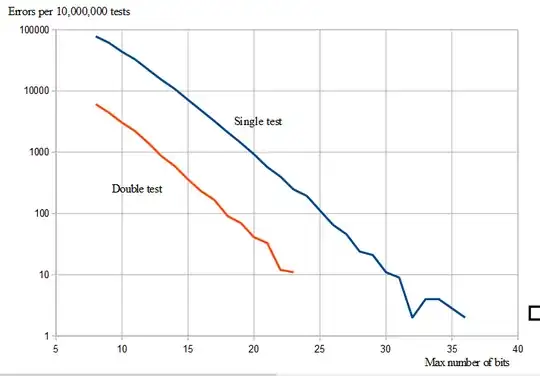
I tested the Rabin-Miller pseudo prime algorithm using a single test value and found that the number of false calls depends on the size of the number to test, reducing to a (conjectured) negligible probability of error for very large numbers.

A number is randomly chosen to be tested. If the number is $0,1,2,3$ or even the correct result is returned. If the number is odd and $>3$ the Rabin-Miller algorithm specified below is used. The result is compared with table values. This algorithm use a random number $a$ for the test. It would never miss a prime but occasionally report a composite to be a prime. If the test is erroneous an error is returned. I used the method at oeis A014233 where a method for exact testing of primes using multiple Rabin-Miller tests is described, together with squeezed prime tables, to assess the truth of primality.

For each $b$ I ran the test $10,000,000$ times with pseudo random numbers less than $2^b$ and then got the following number of errors $e$:

  e      b    f
78144    8  78125
61425    9  55243
43642   10  39063
32688   11  27621
22201   12  19531
15190   13  13811
10789   14   9766
 7176   15   6905
 4814   16   4883
 3227   17   3453
 2122   18   2441
 1422   19   1726
  926   20   1221
  574   21    863
  400   22    610
  247   23    432
  194   24    305
  112   25    216
   65   26    153
   46   27    108
   24   28     76
   21   29     54
   11   30     38
    9   31     27
    2   32     19
    4   33     13
    4   34     10
    0   35      7
    2   36      5
    0   37      3
    0   38      2
    0   39      2
    0   40      1
    0   41      1

The f-column is the function $f(b)=1250000\cdot 2^{-\frac{b}{2}}$.

The algorithm used is:

To test an odd number $n$, write $n=2^r\cdot s+1$, where $s$ is odd.
Given a random number $a$ such that $1<a<n$, if
1. $a^s\equiv 1(\text{mod}\; n)$ or
2. it exists an integer $j$: $0\le j<r$ with $a^{2^j\cdot s}\equiv -1(\text{mod}\; n)$
then $n$ is pseudo prime.

The conjecture is:

For $b$ big enough $\text{e}<1250000\cdot 2^{-\frac{b}{2}}$.
And specially, $\text{e}\sim 2^{-\frac{b}{2}}$.

I intend to use the algorithm for testing big integers and it seems like just one test is enough for $b>256$ since $f(256)=\frac{1}{272225893536750770770699685945414}\,$, which is supposed to be the probability for an error within 10,000,000 random primary tests. For $b<<256$ one can use multiple tests or an exact algorithm.

But how to prove the conjecture or at least make it resonable?

I will also reward an indepentent computer test, that support or not support my own computer test.

I made a test with double check of Rabin-Miller and made a diagram: Blue is single check and red is double check.

Lehs
  • 14,252
  • 4
  • 28
  • 82
  • I think part 1 of your test should read: $a^s \equiv 1 \pmod n$. – Joffan May 29 '16 at 18:54
  • @Joffan: Thanks, you are right! – Lehs May 29 '16 at 19:34
  • I don't understand what $e$ is. I would think that an "error" is a composite number that passes the test (for one base?). But how can you have $78144$ errors for $b = 8$, when there are only $256$ positive integers $\leqslant 2^8$? – Daniel Fischer May 29 '16 at 19:42
  • @DanielFischer: the test repeats with different random numbers for $a$ in the algorithm. And yes, an error is when a composite flags for prime. – Lehs May 29 '16 at 19:48
  • @Lehs how do you choose $a$? Do you only use one value of $a$? – Joffan May 29 '16 at 19:51
  • @Joffan, no I'll try no clearify. Rectangular pseudo numbers between $1$ and $n$ are used for $a$. Each test is random based. – Lehs May 29 '16 at 20:00
  • @DanielFischer: for small $b$ the combinations of random numbers $(n,a)$ are $<< 10,000,000$ and the same combinations occure several times. – Lehs May 29 '16 at 20:06
  • Okay, so for small $b$, you basically check all odd numbers, and all possible bases for these numbers. Several times even, for the smallest $b$s. Thus you find all pseudoprimes and all corresponding bases [maybe not really all, but close]. For large $b$, you test only a small fraction of the odd numbers $\leqslant 2^b$, and only one base for each. For most composites $n$, the number of bases $a$ such that $n$ is a strong (Fermat) pseudoprime to base $a$ is really small. So the chance to accidentally hit one of those combinations is small. – Daniel Fischer May 29 '16 at 20:07
  • 1
    But for every base, there are infinitely many strong (Fermat) pseudoprimes. One test is not enough to be sure you have a prime, but it makes it probable. Any fixed number of tests is not enough to be sure you have a prime. – Daniel Fischer May 29 '16 at 20:07
  • @DanielFischer, the test runs for any number. It check 0,1,2,3 and even and then run the algorithm. The point is that the probability for a random based test to be a false prime seems to depend on the size of the number in a certain way. – Lehs May 29 '16 at 20:18
  • Sorry, I don't understand. Can you describe more precisely what you do? You pick a $b$, and then do you create ten million pseudo-random pairs $(n,a)$ with $1 < a < n \leqslant 2^b$ to check whether $n$ is a strong base-$a$ pseudoprime, or do you create ten million $n \leqslant 2^b$ and test each $n$ with multiple bases? And what does "It check 0,1,2,3 and even" mean? – Daniel Fischer May 29 '16 at 20:35
  • @DanielFischer: I have edited. – Lehs May 29 '16 at 20:58
  • @Lehs I'm still not fully understanding how you pick $a$. Your text now says "a random number" but your earlier comment said "Rectangular pseudo numbers between $1$ and $n$ are used for $a$". Can you clarify? Do you mean that $a$ is chosen with equal probability from the set ${2,3,4,…,n−1}$? – Joffan May 30 '16 at 16:52
  • @Joffan. Yes the last is right, as in the algorithm. – Lehs May 30 '16 at 17:12
  • I don't think your links to that OEIS entry or (your?) blog about prime counting in Forth are sufficiently useful to give as the opening paragraph. When you ask finally "But how to prove the conjecture or at least make it resonable?", the Reader must search back for the conjecture statement. There one finds an inequality relating $b$ and $e$ which is not self-contained. Your specification of "the algorithm" is welcome, but it only defines a strong primality test for one base $a$. It does not correspond well to the OEIS entry (which concerns testing against mutiple bases). – hardmath May 30 '16 at 19:10
  • @hardmath - I think I understand the author's intent and have edited to clarify. The OEIS reference had undue prominence; it's the method used to establish the truth of primality. – Joffan May 30 '16 at 19:30
  • @Joffan: Your edits make the material flow much better. I was making some more conservative edits (punctuation, etc.) that conflicted chronologically with yours. At this point I'll wait to see if the OP weighs in. – hardmath May 30 '16 at 19:34

1 Answers1

3

The Question asks about the distribution of (odd composite) strong pseudoprimes $n$ to a base selected randomly (uniformly) from the set $\{2,\ldots,n-1\}$.

The problem has been studied in the literature. A theoretical upper bound for the probability $p_{b}$ of a $b$-bit odd number $n\gt 1$ chosen at random (uniformly sampled) that passes the strong pseudoprime test to a random base chosen from $\{1,2,\ldots,n-1\}$ is composite is:

$$ p_b \le b^2 4^{2-\sqrt{b}} \;{ when }\; b \ge 2$$

as established by Damgård, Landrock, and Pomerance: Average Case Error Estimates for the Strong Probable Prime Test in Mathematics of Computation Vol. 61, No. 203 (July 1993). Note that they allow the choice of base $a=1$, for which any odd composite will pass a strong pseudoprime test, thereby increasing the chance of a false positive.

But this bound is much weaker than the empirical bounds that can be found. For example, the above authors also report numerically that $p_{600} \le 2^{-75}$, while their theoretical bound above gives roughly $p_{600} \le 2^{-26}$.

Added:

While it is understandable that one might exclude base $a=1$ because it gives a trivial "strong-pseudoprime test" that always succeeds, the same is true of $a=n-1$. So why not exclude that as well?

In randomly sampling the bases $a$ between $1$ and $n-1$ we introduce an element of uncertainty that complicates our analysis. If more than one base were being used in our testing, e.g. sampling bases without replacement, an advantage would be more evident.

I'd like to support conjectured form of a chance of "error", i.e. that a number $n$ passing the Miller-Rabin (base $a$-strong pseudoprime) test yet is composite, by taking that random element out of the procedure and giving exact rather than sampled probabilities. To this end let's settle for the sake of discussion on $a=2$ as our base. After all, we are computing the test only for odd numbers $n$, and automatically the choice $a=2$ is coprime to $n$.

Further counting 2-strong pseudoprimes versus odd primes have been exhaustively worked out to $2^{64}$, so it makes sense to define the probability of "false success" error in a base $a=2$ test for odd numbers up to $n$ as:

$$ \frac{\text{ # of 2-strong pseudoprimes } \le n}{(\text{ # of 2-strong pseudoprimes } \le n) + (\text{ # of odd primes } \le n)} $$

The graph below is driven by data generated at increments $n = 10^k$, and then taking the negative (common) logarithm (i.e. base ten) of the probability so defined. I find the interpretation of common logs in terms of decimal places easier to grasp, but here the key characteristic is the slope of the trend line:

frequency of 2-strong pseudoprime composites among primes

Fig. 1 Graph of -log probability odd number passing 2-strong PrP is composite

This slope is roughly the one-half conjectured by OP, i.e. $e = O(2^{-b/2})$, and doesn't depend on whether base two or base ten is being used for increments. If anything the slope seems slightly steeper than one-half, so that the chance of error is dropping a little faster.

However this doesn't convey to me that a single Miller-Rabin test is "good enough", but rather that one such test is quite efficient in weeding out composites. A follow-on test, perhaps of an entirely different kind, is worth doing if one really wants to drive the chance of "false positive" error for primality into negligible magnitudes.

Here are the counts of $2$-strong pseudoprimes and odd primes below the indicated $10^k$ increments, summarized from the sources linked above and used to create the scatter plot and trendline with Google Sheets:

$$\begin{array}{r|r|r} k & \text{# 2-strong pseudoprimes } \lt 10^k & \text{# of odd primes } \lt 10^k \\ \hline 4 & 5 & 1228 \\ 5 & 16 & 9591 \\ 6 & 46 & 78497 \\ 7 & 162 & 664578 \\ 8 & 488 & 5761454 \\ 9 & 1282 & 50847533 \\ 10 & 3291 & 455052510 \\ 11 & 8607 & 4118054812 \\ 12 & 22407 & 37607912017 \\ 13 & 58892 & 346065536838 \\ 14 & 156251 & 3204941750801 \\ 15 & 419489 & 29844570422668 \\ 16 & 1135860 & 279238341033924 \\ 17 & 3115246 & 2623557157654232 \\ 18 & 8646507 & 24739954287740859 \\ 19 & 24220195 & 234057667276344606 \end{array} $$

Table 1: Counts of 2-strong pseudoprimes and odd primes up to $10^k$

hardmath
  • 37,715
  • 1
    I don't think the choice of $a=1 $ is allowed. I did ask about the selection range of $a$. – Joffan May 30 '16 at 22:35
  • I will rephrase what I wrote. I was reporting on what was done in the paper, and of course one can improve (decrease) the likelihood of a false positive if $a=1$ is excluded. – hardmath May 30 '16 at 23:44
  • Thanks all of you! The question was a bit messy. Interesting that my experiment gives so much smaller emiprical errors than the empirical errors of the computer scientists above. My function $f$ isn´t based on anything but "looks" good. – Lehs May 31 '16 at 00:20
  • @Joffan. I got the algorithm from http://mathworld.wolfram.com/Rabin-MillerStrongPseudoprimeTest.html but thought that the case $a=1$ was a typo, so I changed to $1<a$. – Lehs May 31 '16 at 00:25
  • 2-strong pseudoprime means that the base $a=2$ case Miller-Rabin test succeeds for a composite, rather than for an actual prime. So the probability of "error" is the fraction of these among all (odd number) cases where the test for base $a=2$, i.e. their count plus the number of actual (odd) primes. – hardmath Jun 05 '16 at 13:10