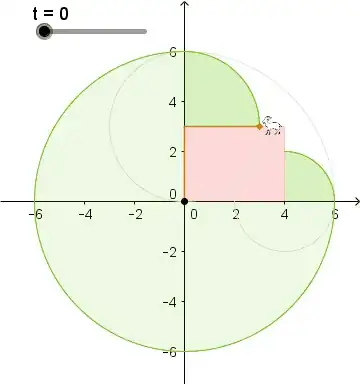
Here are some hints.
First, draw a rectangle $3$ cm high and $4$ cm wide. It should look like Achille Hui's diagram.)
Now, draw a line $6$ cm long from the lower left corner into the yard.
Now look at the area that the goat can go without catching the rope on the upper left corner, or on the lower right corner. What shape is it? (Think $9$ slices of a $12$-slice pizza.) What is the area? (The area of a full circle is $\pi r^2$, with $\pi \approx 3.14$ and $r$ being the radius of the circle.)
Now, if the goat is really hungry, it can go around to the right side of the house, or around to the top side of the house. How much rope is free on the top? (Think $6$ m - $3$ m.) What is the area of the patch that the goat can reach around with this amount of rope?
What about the bottom part? (Think $6$ m - $4$ m.)
Can you take it from here?