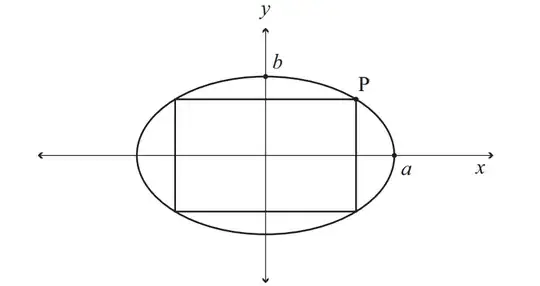
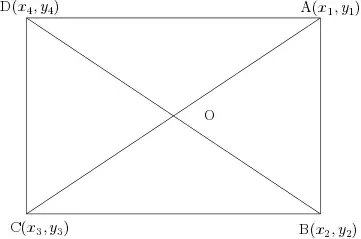
Suppose we have a rectangle which has all four vertices on the ellipse. If $C$ is the center of the rectangle, then all vertices of the rectangle are in the same distance from $C$. If we choose coordinate system with origin in the point $C$, we get the equation
$$x^2+y^2=r^2.$$
We also want to express the condition that the vertices belong to the ellipse. So far we have only chosen the origin of our Cartesian coordinate system to be the point $C$. We can also choose the axes to be parallel to the axes to the ellipse. If we denote by $(x_0,y_0)$ the center of the ellipse, we get the equation
$$\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1.$$
Since rectangle is centrally symmetric w.r.t. the point $C=(0,0)$, the vertices also lie on an ellipse which is centrally symmetric to the ellipse described above. This si precisely the ellipse
$$\frac{(x+x_0)^2}{a^2}+\frac{(y+y_0)^2}{b^2}=1.$$
So we got the following three equations:
\begin{align}
x^2+y^2&=r^2 \tag{1}\\
b^2(x-x_0)^2+a^2(y-y_0)^2&=a^2b^2 \tag{2}\\
b^2(x+x_0)^2+a^2(y+y_0)^2&=a^2b^2 \tag{3}
\end{align}
We are asking for the conditions on $x_0$, $y_0$ and $r$ such that there are at least four solutions.
Notice that by subtracting the equations $(2)$ and $(3)$ we get
$$b^2xx_0+a^2yy_0=0.\tag{4}$$
Let us first show that $x_0=y_0=0$. Assume that this is not true. For example, let us assume $x_0\ne0$. Then we get
$$x=\frac{a^2y_0}{b^2x_0}\cdot y. \tag{5}$$
By plugging $(5)$ into $(1)$ we get
$$y^2\left(1+\frac{a^2y_0}{b^2x_0}\right)^2=r^2 \tag{6}$$
which gives us two possibilities for $y$. Combining this with $(5)$ we get two possibilities for the point $(x,y)$.
So we see that if $x_0\ne0$, then there are at most two solutions of the above system. The case $y_0\ne0$ is symmetric. In order to get a rectangle we need at four points, so we necessarily have1
$$x_0=y_0=0.\tag{7}$$
In the other words, we have found out that the center of the rectangle and the center of the ellipse coincide.
This condition significantly simplifies the original system to
\begin{align}
x^2+y^2&=r^2 \\
b^2x^2+a^2y^2&=a^2b^2
\end{align}
From the first equation we get $y^2=r^2-x^2$. By plugging this value into the second equation we get
\begin{align}
b^2x^2+a^2(r^2-x^2)&=a^2b^2\\
(b^2-a^2)x^2&=a^2(b^2-r^2)
\end{align}
Since we do not consider the case $b=a$, which corresponds to the ellipse being circle, we get
$$x^2=\frac{a^2(b^2-r^2)}{b^2-a^2}.$$
Assuming the RHS is positive, this gives us two possible values $$x=\pm\sqrt{\frac{a^2(b^2-r^2)}{b^2-a^2}}.$$
From these values we can get $$y=\pm\sqrt{r^2-x^2}$$
(again assuming that $r^2-x^2>0$).
Clearly, we got a rectangle with the sides parallel to the axes. (The vertices of rectangle have the form $(x_1,y_1)$, $(-x_1,y_1)$, $(-x_1,y_1)$, $(-x_1,-y_1)$.)
In fact, using the above equations we can also find the conditions on $a$, $b$ and $r$ when the intersection exists. W.l.o.g. we can assume $0<a<b$. (The other case is symmetric.) If we want $a^2(b^2-r^2)/(b^2-a^2)$ to be positive, we need $r<b$.
We also need
$$0<r^2-x^2 = r^2- \frac{a^2(b^2-r^2)}{b^2-a^2} = \frac{a^2(b^2-r^2)}{b^2-a^2} = \frac{b^2(r^2-a^2)}{b^2-a^2}$$
which gives us $a<r$.
So we get a solution only if
$$a<r<b$$
as expected.
1Another possibility how to view the case $(x_0,y_0)\ne(0,0)$, i.e. the case when the center of the rectangle is different from the center of the ellipse, is that in such case we can only get a line segment - which could be considered as a "rectangle having zero width".