Roots of the Taylor approximation of the exponential

Asked May 04 '16 at 22:20

Active May 04 '16 at 22:26

Viewed 56 times

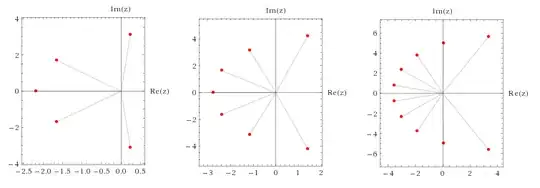
While answering another question, I looked at the roots of the $n^{th}$ degree Taylor approximation of the exponential.

$$e^x\approx E_n(x):=\sum_{k=0}^n\frac{x^k}{k!}.$$

Apparently, these root are aligned on a parabola-like smooth curve depending on $n$.

How would you address the problem of finding the equation of this curve, ignoring the exact positions of the roots along it ?

edited May 04 '16 at 22:26

asked May 04 '16 at 22:20

1

A neat answer by JM and some references. – Raymond Manzoni May 04 '16 at 22:34
@RaymondManzoni: splendid ! – May 04 '16 at 22:38
Glad you liked it! Cheers, – Raymond Manzoni May 04 '16 at 22:43
1

@RaymondManzoni: now, as these roots are the same as those of the incomplete Gamma $\Gamma(n+1,z)$, we even have a way to study a non-integer number of roots :) – May 04 '16 at 22:48

0 Answers0