4

How would you divide an octagon into 5 equal parts?

This is a question that we are working on in 2nd grade. Do you have an answer for us?

Thanks, Mrs. Parsons Class West View Elementary Burlington, Wa

Parsons 2nd Grade
  • 41
  • 5
    I assume you mean regular octagon. How are those 5 parts equal? Same area? Same size and shape? Can they be mirrored? – flawr May 03 '16 at 19:46
  • 1
    Divide the octagon into eight triangles, then each triangle into 25 sub-triangles (divide each side into five parts, so you get $1+3+5+7+9$ sub-triangles in each triangle). There are then 200 equal subtriangles. Since $200 = 40\cdot5$, divide the subtriangles into groups of 40 each. – Nominal Animal May 04 '16 at 00:31
  • 3
    This is surprising. And your students won't believe it maybe. But if you measure the perimeter (let's say it's 40 inches-- 5 inches to a side). Divide into 5. (say 8 inches). Start anywhere and measure that distance 5 times. Each wedge will be equal. – fleablood May 29 '16 at 00:02

3 Answers3

3

If your intention is to divide a regular octagon into five regions of equal area, see the figure below:

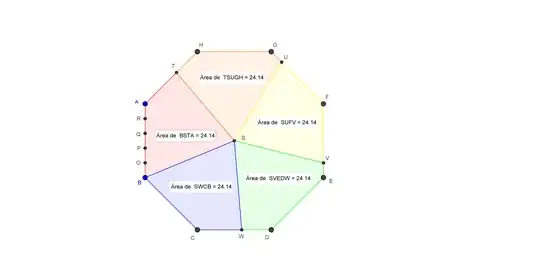OctagonDivFive At first divide side $AB$ (length 5 units) into five equal segments ($BO, OP, PQ, QR$ and $RA$).

Then mark points $T, U, V$ and $W$ on the sides of the octagon, so that $AT=BQ$, $GU=BO$, $FV=BR$ and $DW=BP$.

At last draw the segments $ST, SU, SV, SW$ and $SB$, where $S$ is the center of the ocatagon.

RicardoCruz
  • 3,743
1

Let $ABCDEFGH$ be the octagon. Go $2/3$ of the way from $A$ to $B$ on side $AB$ and construct an auxiliary line segment from that point to the midpoint of $DE$. Then construct successive $45°$ rotations of this segment around the center of the octagon.

You create a smaller octagon in the center, whose area measures $1/5$ that of $ABCDEFGH$. That is one of your parts. To get the other four parts use symmetry to divide the area between the octagons into four pieces.

Oscar Lanzi
  • 48,208
1

Draw a square in the center whose area is a fifth of the octagon's area. Then connect it to the octagon with 4 symmetric lines.

Interactive demonstration

octagon subdivided in 5 regions, style 1

If you rotate it so that the square's sides are parallel to (half of) the octagon's sides, it looks like the side length of the square is the same as that of the octagon! If this came from a textbook, perhaps this is the intended solution, I thought! However, it's not correct. The side length of the octagon is about 1.7% larger than that of the square, in order to maintain equal area, making this is a valid but misleading solution:

octagon subdivided in 5 regions, style 2

However, the solution space is wide...

The lines connecting the center shape to the octagon don't have to align directly with the vertices of the octagon or center shape, they just have to be rotationally symmetric, and span between the shapes. They could even be curved, if you want to get creative with it!

The center shape doesn't have to be a square, it can be a circle or any shape as long as it has 4 lines of symmetry, and fits within the octagon. A star shape that reaches the bounds of the octagon might be another interesting solution.

1j01
  • 146
  • 2
    Area of octagon / area of square is not $5$: https://geogebra.org/geometry/jkqa8ptx. But the first solution works just fine. – Lucenaposition Aug 25 '24 at 22:50
  • Interesting! So it's an illusion... To be clear, my second graphic also shows a valid division, but the lines aren't quite the same length like I had assumed, making it rather misleading. I almost checked it, but I didn't. I'll update my answer. – 1j01 Aug 25 '24 at 23:17
  • Updated. I also updated my interactive demo to add right angle indicators and, more importantly, near-right-angle warnings. Thanks for checking my work @Lucenaposition – 1j01 Aug 26 '24 at 00:31