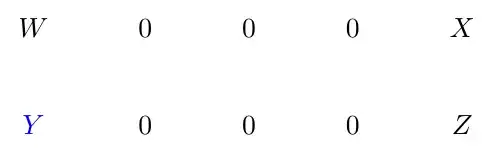What comes after diagram chasing?

Question

An early edition of Lang's algebra textbook gives the famous exercise to

Take any book on homological algebra, and prove all the theorems without looking at the proofs given in that book.

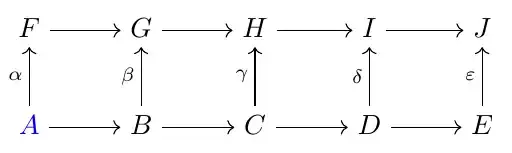
Here are some of theorems you would find in such a book: the snake lemma, the five lemma, the nine lemma, the many unnamed lemmas for constructing long exact sequences in algebraic topology (e.g. Mayer-Vietoris). The only way I know to prove these theorems, and which I have read in homological algebra books, is by a diagram chase.

I have nothing against diagram chasing -- it's rather fun once you figure out how it works. But it also feels rather mechanical and devoid of insight.

1. Is there any systematic way to think about/prove/remember theorems in homological algebra like the ones that I cited without having to resort to diagram chasing?
2. Are the theorems of the type I mentioned small enough in number to be subsumed by some general theory which explains them?
3. Is homological algebra anything more than a mindless subject used for its applications in other areas of math?

A satisfactory answer would allow us to (for instance) look at the hypotheses of the five lemma and then see immediately that the vertical arrow is an isomorphism.

Note: I am aware of the formalism of abelian categories, though not yet a competent user. It seems to me that abelian categories generalize the setting of homological algebra without clarifying its content. For instance, it seems like most people, when pressed to prove theorems of the type I mentioned in an abelian category, use Mitchell's Embedding Theorem to justify performing a diagram chase.

Answer 1

I highly recommend reading through Ravi Vakil's notes on spectral sequences. For convenience I'll outline the general points relating spectral sequences to diagram lemmas.

Diagram lemmas usually begin with a double complex. That is a grid of maps

composing to $0$. Here the blue bullet denotes the $(0,0)$ position (or the "origin") of the grid. This grid is called the "$0$th page" of the spectral sequence, or $E_0$.

Spectral sequences supply us with two different ways of studying this grid. We can think "vertically" or "horizontally". Each perspective supplies us with an algorithm.

The "horizontal" perspective is an algorithm where we start by replacing each object in $E_0$ with its corresponding homology obtained from the horizontal arrows. This gives us a new grid of objects, $_{>}E_1$. Additionally, this new grid is supplied with differentials that now point "up". We continue this process, taking homology and inheriting a differential to obtain new "pages". The direction of the differential on the $_{>}E_r$ page is $_{>}d_r:E_r^{p,q}\to E_r^{p-r+1,q+r}$. Thus the differentials "spiral out in a counter-clockwise fashion"

On the other hand, we can think "vertically" and obtain a similar algorithm. Take homology to obtain new grids $_{\hat{}}E_r$, starting with the vertical maps. The differentials in this case "spiral out in a clockwise fashion"

The idea of spectral sequences roughly states:

The two collections of grids $_{>}E_r$ and $_{\hat{}}E_r$ eventually stabilize to the same grid $E_{\infty}$.

This gives us a surprisingly powerful tool for studying diagram lemmas. For example, let's prove the 5-lemma. Suppose we have a diagram

with exact rows where $\alpha$, $\beta$, $\delta$, and $\varepsilon$ are isomorphisms.

The first page of the horizontal homology $_{>}E_1$ is

where the $\bullet$'s are the only objects that are not necessarily zero. The next page $_{>}E_2$ is

The maps here are omitted because they are all necessarily zero! From here we see that the spectral sequences converges to $E_{\infty}=_{>}E_2$ since the only possibly nonzero objects have differentials entering and exiting zero objects from page two onward.

Now, the first page of the vertical homology $_{\hat{}}E_1$ is

The vertical pages stabilize immediately. Thus we see that $_{\hat{}}E_1\simeq _{>}E_2\simeq E_\infty$. In particular, $\ker\gamma\simeq\DeclareMathOperator{cok}{cok}\cok\gamma\simeq0$. Hence $\gamma$ is an isomorphism.

The moral here is: if we accept the theory of spectral sequences as a black box, then many diagram lemmas are quite natural.