8

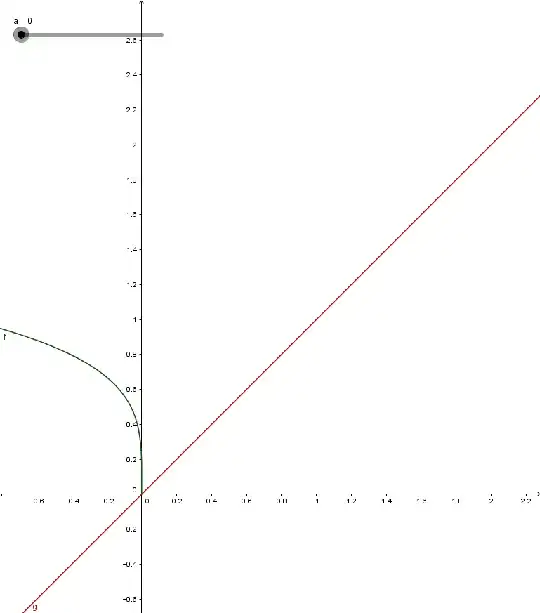
For a real number $a>0\;,$ How many real solution of the equation $\sqrt{a+\sqrt{a-x}} = x$

$\bf{My\; Try::}$ We can Write $\sqrt{a+\sqrt{a-x}} = x$ as $a+\sqrt{a-x}=x^2$

So we get $(x^2-a)=\sqrt{a-x}\Rightarrow (x^2-a)^2 = a-x\;,$ Where $x<a$

So we get $x^4+a^2-2ax^2=a-x\Rightarrow x^4-2ax^2+x+a^2-a=0$

Now How can i solve it after that, Help me

Thanks

juantheron
  • 56,203
  • If you are really desperate there is the formula for quartic polynomials but I'm sure you know. –  Apr 24 '16 at 02:40
  • Relevant: http://math.stackexchange.com/questions/785/is-there-a-general-formula-for-solving-4th-degree-equations/1219804#1219804 – Nicholas Stull Apr 24 '16 at 02:46
  • @NicholasStull - not really... –  Apr 24 '16 at 03:19
  • @Αδριανός - Why those functions, and not the ones in the initial equation? With what you graphed you may get solutions that weren't solutions of the original one (remember you squared both sides)! –  Apr 24 '16 at 03:20
  • @mathguy Yeah you're absolutely right. I was messing around trying to rewrite it in a solvable form before I finally gave up and graphed it. It is probably easier then to just graph the original function instead of worrying about a handful of new inequalities to make my comment valid. – KR136 Apr 24 '16 at 03:24
  • @Αδριανός - When you posted your comment, I had already essentially done exactly that in my Answer (and rigorously, too). –  Apr 24 '16 at 03:51
  • @mathguy Perhaps I was not clear enough in my intention: I meant to extol the virtue of looking graphically at the problem. Your answer effectively does that, but I wanted to add that sometimes it is helpful, in order to understand your explanation, to actually see the thing itself. – KR136 Apr 24 '16 at 03:53

4 Answers4

5

You get a quadratic equation in terms of "$a$". Using the quadratic formula for $a$, $$ a=\frac{2x^2+1\pm|2x-1|}{2} $$ From this, we get $a=x^2+x$ or $a=x^2-x+1$, so $$ x=\frac{-1\pm \sqrt{1+4a}}{2}\text{ or } x=\frac{1\pm\sqrt{-3+4a}}{2} $$ Now we must get rid of possiblities:

  • If $x=\frac{-1-\sqrt{1+4a}}{2}$, it violates $x\ge 0$.
  • If $x=\frac{-1+\sqrt{1+4a}}{2}$, it must satisfy $\frac{-1+\sqrt{1+4a}}{2}\ge \sqrt{a}$, which has no roots.
  • If $x=\frac{1-\sqrt{-3+4a}}{2}$, it must satisfy $\frac{1-\sqrt{-3+4a}}{2}\ge\sqrt{a}$, which has no roots.

The only remaining possibility is $x=\frac{1+\sqrt{-3+4a}}{2}$. Solve below inequality: $$ \sqrt{a}\le \frac{1+\sqrt{-3+4a}}{2}\le a $$ Solving left inequality, we get $a\ge 1$, and solving right inequality, we get $4(a-1)^2\ge 0$. Thus the root of given equality when $a\ge 1$ is $$ x=\frac{1+\sqrt{-3+4a}}{2}\;(a\ge 1) $$ If $0<a<1$, then there are no roots.

enter image description here

choco_addicted
  • 8,906
3

Sometimes you don't need to solve an equation to determine how many solutions it has in a certain domain.

For x real, the RHS is real so the LHS must also be real, from which you find $x \le a$. Now: for $x = 0$ the LHS is strictly positive and the RHS is 0. The LHS is strictly decreasing and the RHS is strictly increasing, so you have either zero or one solution depending on how the LHS and the RHS compare at $x=a$. So it depends on whether $\sqrt a \le a$ or $\sqrt a > a$.

1

It factors!

$x^4-2ax^2+x+(a^2-a)=(x^2+x-a)(x^2-x+(1-a))$

How do I get that? Well, there will be an extraneous root with the wrong signs for the inner square root, thus:

$x=\sqrt{a-\sqrt{a-x}}$

$-x=-\sqrt{a-\sqrt{a+(-x)}}$

The second extraneous equation is consistent with the simpler recursion

$y=-\sqrt{a+y}$

with $y=-x$. So upon squaring the last equation we find that $y^2-y-a=x^2+x-a=0$ meaning the quadratic expression must be a factor of the quartic.

But perforce it is the wrong factor. The intended roots must be in the complementary quadratic factor

$(x^2-x+(1-a))=0$.

Oscar Lanzi
  • 48,208
  • Be careful though - since we squared the initial equation a couple of times, not all the solutions of the quartic equation will necessarily satisfy the original equation. –  Apr 24 '16 at 03:17
  • So you have to identify the correct factor. A hint is in my updated answer. – Oscar Lanzi Apr 24 '16 at 03:22
  • 1
    Not sure you noticed, I already showed in my Answer there is either no solution or exactly one, depending on whether $a>1$ or $a \le 1$. –  Apr 24 '16 at 03:52
  • So we are left with the quadratic roots we would have to check for the proper signs on the radicals. Looks like one solution for $a\geq1$ (including the equality). – Oscar Lanzi Apr 24 '16 at 05:16
0

Firstly, let's say $f(x) = \sqrt{a+\sqrt{a-x}} - x$. If $f$ has real solutions, then it must hold that $x \in [0,a]$. Now, taking the derivative of $f$, we have: $$f'(x) = -1-\dfrac{1}{4\sqrt{a+\sqrt{a-x}}\cdot (\sqrt{a-x})}.$$

Clearly, $f'(x)<0, \forall x \in [0,a).$ Thus, $f$ is strictly decreasing in $[0,a]$.

Also, we have that $f(0) = \sqrt{a+\sqrt{a}}>0, \, \forall a>0$. Moreover, $f(a) = \sqrt{a} - a$. Thus, everything depends on the value of $a.$

Thus, there will be either zero roots or one root of $f$.

thanasissdr
  • 6,408
  • @OscarLanzi - if you would read my Answer you would see there can't be more than one root. For a trivial reason. –  Apr 24 '16 at 03:53
  • @OscarLanzi http://www.wolframalpha.com/input/?i=Plot%5BSqrt%5B0.8125%2BSqrt%5B0.8125-x%5D%5D-x,%7Bx,0,0.8125%7D%5D Here's the graph of $f$ when $a=0.8125$. I totally agree with mathguy. – thanasissdr Apr 24 '16 at 03:55
  • Deleted my comment. – Oscar Lanzi Apr 24 '16 at 04:35