14

The problem i came across is the evaluation of $$\int_0^\infty\frac{\sin x}{x}\,dx$$ I chose the function $f(z) = \dfrac{e^{iz}}{z}$ and took a contour of $[\varepsilon , R ] + [R , R+iy] + [-R+iy , R+iy] + [-R,-R+iy]+[-R, -\varepsilon]$ . The problem is how do I continue now to find integrals on each of these segments ?

Mathslover shah
  • 593
  • 1
    An aside, unrelated to the question: for one of my favorite integral tricks, look up Feynman's trick-- or, more objectively, "differentiating parameters under an integral." One of the classic examples is solving this integral without complex analysis. (Hence its unrelated-ness). – KR136 Apr 12 '16 at 21:52
  • Why did you choose the $f(z) = \dfrac{e^{iz}}{z}$ , does $sin(x)=e^{iz}$ ? – Zophikel Feb 24 '18 at 18:13

1 Answers1

17

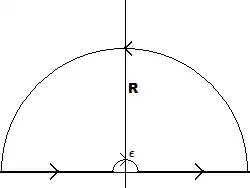
Take the function $\;f(z)=\frac{e^{iz}}z\;$ and define the (positive) indented semicircle

$$\gamma_r:=\{z\in\Bbb C\;:\;z=re^{it}\;,\;\;0\le t\le \pi\,,\,\,r>0\}$$

Now, for big $\;R\in\Bbb R_+\;$ and very small $\;\epsilon>0\;$ , take the contour:

$$C:=[-R,-\epsilon]\cup(-\gamma_\epsilon)\cup[\epsilon,R]\cup\gamma_R$$

We're going to use the lemma, and in particular its corolary, that in the first and most upvoted answer here

enter image description here

Observe that $\;f\;$ is analytic on the contour and within the domain enclosed by it, so by Cauchy's Theorem its integral equals zero. Also

$$\text{Res}_{z=0}(f)=\lim_{z\to 0} zf(z)=e^0=1$$

and thus by the lemma

$$\lim_{\epsilon\to0}\int_{\gamma_\epsilon}f(z)=\pi i$$

and also

$$\left|\int_{\gamma_R}f(z)\,dz\right|\le\frac{\pi R e^{-R\cdot\text{Im}\,z}}{R}\xrightarrow[R\to\infty]{}0\,,\,\text{since}\;\;\text{Im}\,(z)>0\;\;\text{on}\;\;\gamma_R$$

So we get:

$$0=\oint_C f(z)\,dz=\int_{-R}^\epsilon f(x)\,dz-\int_{\gamma_\epsilon} f(z)\,dz+\int_\epsilon^R f(x)\,dx+\int_{\gamma_R}f(z)\,dz\implies$$

$$0=\lim_{R\to\infty,\,\epsilon\to0}\oint_C f(z)dz=\int_{-\infty}^\infty\frac{e^{ix}}xdx-\pi i$$

and now just compare imaginary parts and divide by two since the real function is even.

DonAntonio
  • 214,715
  • 4
    How exactly do you deduce $\operatorname{Im}(z) > 0$ on $\gamma_R$? I think you have only that $\operatorname{Im}(z) \geq 0$ and in this case you wouldn't get the convergence to $0$. – Yaddle Jun 14 '17 at 14:01
  • @Yaddle That's definition of $;\gamma_R;$ and it really doesn't matter for convergence. If you want change to $;0<t<\pi;$ , it doesn't matter. – DonAntonio Apr 16 '18 at 04:25
  • 2
    How do you get the bound of the integral on $\gamma_R$? – Connor Apr 29 '18 at 00:51
  • 1
    @Connor You can use Jordan's Lemma: https://en.wikipedia.org/wiki/Jordan%27s_lemma , or the l.m. (estimation) lemma: https://en.wikipedia.org/wiki/Estimation_lemma – DonAntonio Apr 30 '18 at 04:57
  • Sir f(z)= $e^{iz}/z$ otherwise I think it will not be bounded – Curious student Nov 03 '18 at 03:49
  • @SRJ Yes, that is what was there: $;f(z)=\cfrac{e^{iz}}z;$ . Of course $;e^{iz};$ doesn't work. Please first write comment, then do edit. – DonAntonio Nov 03 '18 at 13:14
  • The ending is dangerous: $$\int_{-\infty}^\infty\frac{e^{ix}}x,\mathrm dx$$ is only well-defined in the Cauchy principal-value sense since there is a $\frac 1x$ divergence at $x=0$. – Maximilian Janisch Apr 02 '22 at 11:48