3

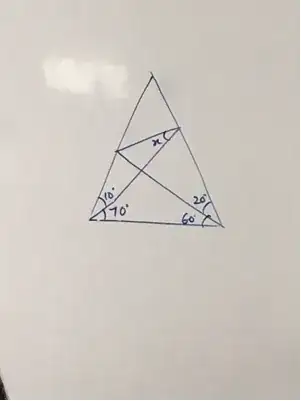
enter image description here I've been solving this for days but I still I couldn't solve this. Can I know how to solve $x$ ?

Blue
  • 83,939
Mathxx
  • 8,468

2 Answers2

2

I fail to see the importance and difficulty of Langley’s Problem mentioned by Justin Benfield in his answer here apart perhaps some historical mention or maybe some interesting applications. In effect, here I give an EASY generalization of the problem proposed by the OP. I would appreciate any substantiated comment against (am I wrong?).

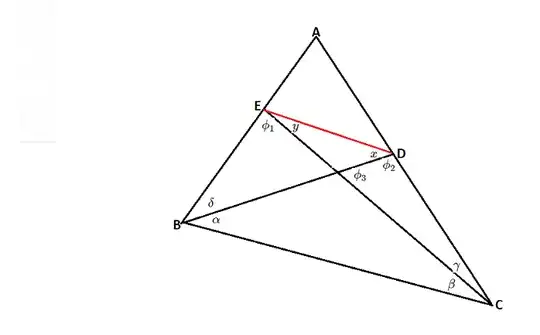
Let $\triangle{ABC}$ not necessarily isosceles. Given side $a$ and angles $\alpha,\beta,\gamma,\delta$ determine the angles $\phi_1,\phi_2,\phi_3,x,y$ as well as the segments $BE,BD,CD$ and the said difficulty would be to determine $x$ or $y$ since $\phi_1,\phi_2,\phi_3$ are immediate to calculate

enter image description here

We have $$BE=\frac{\sin \beta}{\sin \phi_1}\cdot a\\BD=\frac{\sin \phi_3}{\sin \phi_2}\cdot a\\CD=\frac{\sin \alpha}{\sin \phi_2}\cdot a\\ED=BE\cdot\frac{\sin \delta}{\sin x}=\frac{\sin \beta\sin\delta}{\sin \phi_1\sin x}\cdot a $$ It follows the easy system $$\begin{cases}x+y=\phi_3\\\space\\\dfrac{\sin (\phi_1+\phi_3-x)}{\sin x}=\dfrac{\sin\phi_1\sin\phi_3}{\sin\beta\sin\phi_2}\end{cases}$$ This gives an elementary equation of the form $$A\sin x+B\cos x=C$$ one of the quite popular way to solve is the following: $$A\sin x+B\cos x=C\iff\frac{A\sin x}{\sqrt{A^2+B^2}}+\frac{B\cos x}{\sqrt{A^2+B^2}}=\frac{C}{\sqrt{A^2+B^2}}$$ so $$x+\theta= \arcsin{\frac{C}{\sqrt{A^2+B^2}}}\space\text{where } \space \theta=\arccos{\frac{A}{\sqrt{A^2+B^2}}}$$

Ataulfo
  • 32,657
1

Your's is a version of Langley's problem, with slightly different angles. It shouldn't be too difficult to adapt the solution presented here: http://www.gogeometry.com/LangleyProblem.html to your current problem.

Note that this is problem's solution is rather clever, and involves constructing a new edge rather than simple angle chasing (I spent quite a lot of time trying to solve it with angle chasing arguments to no avail before resorting to google searching about it, only to find out that angle chasing didn't cut it, and hence I am now writing this answer).

Justin Benfield
  • 4,118
  • A solution for your variant (that is flipped horizontally from how you have it), can be found here: http://www.cut-the-knot.org/triangle/80-80-20/60-70Sol1.shtml#solution – Justin Benfield Apr 12 '16 at 03:42
  • Sorry I don't understand the solution well... In this website, why ∠BDF = 30°? – Ray Cheng Jun 17 '17 at 11:14
  • It can be shown fairly easily by angle-chasing using the fact that $\angle$BCF was constructed to be $50^{\circ}$. – Justin Benfield Jun 18 '17 at 18:35
  • could you show the details please? – Ray Cheng Jun 19 '17 at 08:37
  • @RayCheng After futzing with the problem for a bit, I realized it's not a matter of simple angle chasing, when the author of what I linked referred to the 'classical framework' he was referring to how the newly constructed edge, and the $60^{\circ}$ angle opposite it, are like the classic version of the problem to which that text links, there you will find 12 different approaches to solving that problem, from that solution, the one to the present problem can be derived in the manner the author describes. – Justin Benfield Jun 26 '17 at 13:19
  • Can you provide the link which states 12 different approaches to solve the problem? – Ray Cheng Jul 08 '17 at 02:21
  • Click on the words Classical Framework, you will taken here: http://www.cut-the-knot.org/triangle/80-80-20/IndexToClassical.shtml – Justin Benfield Jul 09 '17 at 10:57
  • Could you show the detail steps of the 10-70-20-60 triangle please? The website only talks about how to do 30-50-20-60 triangle and I don't know how to apply the method into the 10-70-20-60 triangle. – Ray Cheng Jul 11 '17 at 09:40