33

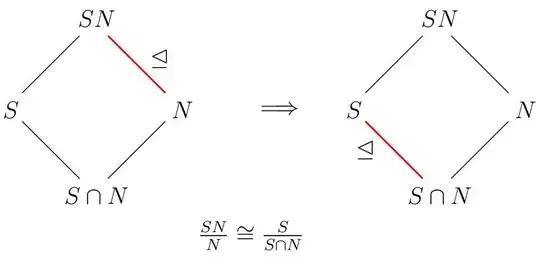
In group theory we have the second isomorphism theorem which can be stated as follows:

Let $G$ be a group and let $S$ be a subgroup of $G$ and $N$ a normal subgroup of $G$, then:

  1. The product $SN$ is a subgroup of $G$.
  2. The intersection $S\cap N$ is a normal subgroup of $G$.
  3. The quotient groups $SN/N$ and $S/(S\cap N)$ are isomorphic.

I've seen this theorem some time now and I still can't grasp an intuition for it. I mean, it certainly is one important result, because as I've seen it is highlighted as one of the three isomorphism theorems.

The first isomorphism theorem has a much more direct intuition though. We have groups $G$ and $H$ and a homomorphism $f:G\to H$. If this $f$ is not injective we can quotient out what is stopping it from being injective and lift it to $G/\ker f$ as one isomorphism onto its image.

Is there some nice interpretation like that for the second isormorphism theorem? How should we really understand this theorem?

Connor
  • 647
Gold
  • 28,141
  • 20
    This isn't "an answer", but I think of it like this: suppose we have a subgroup of $G$, with a normal subgroup $N$. We might want to know "what happens when we quotient out $N$ from some subgroup $H$". The trouble is, $N$ might not be a subgroup of $H$. So we either quotient $N$ out from the smallest subgroup of $G$ containing $H$ and $N$, or we quotient $H$ by the intersection of $H$ and $N$, and both approaches lead us to "the same place". – David Wheeler Apr 12 '16 at 01:49
  • the comment of David Wheeler is expanded upon in an answer here: https://math.stackexchange.com/questions/722632/interpretation-of-second-isomorphism-theorem?rq=1 – D.R. Apr 21 '22 at 06:03

4 Answers4

41

I assume you are having intuitive difficulties with the third statement of the theorem. Let me try and give an intuitive explanation. Every element of $SN$ is of the form $sn$ with $s \in S$ and $n \in N$. Now in $SN/N$ the $n$'s get 'killed' in the sense that in this group $\overline{sn}=\overline{s}$ for $s \in S$ and $n \in N$. However, we are not left with a group that is isomorphic with $S$, because if $s \in N$, that is if $s \in S \cap N$, then $s$ is also the identity in $SN/N$. So, we are left with $S$, but with the remaining part of $N$ completely filtered out, that is $$\frac{SN}{N} \cong \frac{S}{S \cap N}$$

M. Van
  • 4,328
18

Suppose you drop condition that $N$ is normal in $G$. Then $S,N$ are simply subgroups of $G$. In this case, we can say only about equality of number of cosets. $$|SN\colon N| = |S\colon S\cap N|.$$ But when $N$ is normal, then we can certainly talk about quotient, and it is not only by $N$ but also with some other subgroup, and also isomorphism between them (which are statements (1), (2), (3) in question). I think, this situation can be shown better through diagram: enter image description here

If $N$ is normal in $G$, then $N$ should be normal in every subgroup in which it is contained. So, if $S$ is other subgroup, then $N$ is certainly contained in $SN$ and hence $N\trianglelefteq SN$ (left part diagram). The isomorphism theorem you concerned says, then $S\cap N$ is then normal in $S$ (right part diagram) and the corresponding quotient groups (think like-red line sections) are isomorphic.

Proving this isomorphism is elementary algebra; no need to think of any strange map; it is most natural one which everyone can think and so it is, in my opinion, the diagram than the proof of this theorem to be understood in the beginning.

Community
  • 1
p Groups
  • 10,458
  • 1
    Just to clarify one thing: in case $N$ and $S$ aren't normal, $SN$ is not necessarily a subgroup of $G$ (it is if and only if $SN=NS$). But $SN$ is still the union of cosets of $N$, so it makes sense to write $|SN:N|$. – porkynator Jul 16 '16 at 12:50
  • 2
    yes; second the isomorphism theorem was about isomorphism for some quotients, for which, normality of one subgroups is necessary and sufficient. – p Groups Jul 17 '16 at 05:09
7

We have a surjective homomorphism $$f : S \to \frac{SN}{N}$$ given by $f(s) = sN$. We have $\ker(f) = S \cap N$, so $$\frac{S}{S \cap N} \cong \frac{SN}{N}$$ In other words, if $f$ is not injective, we quotient out by the kernel to obtain an isomorphism, exactly as we do to prove the first isomorphism theroem. In other words, we would like each coset $sN \in SN/N$ to correspond to $s \in S$. But if $s \in N$, then $sN = N$, so it instead corresponds to a coset $s(S \cap N) \in S/(S \cap N)$

Ethan Alwaise
  • 9,528
3

There are two additional facts that, in my opinion, make this somewhat more obvious. First,

  • Let $\pi$ be the projection map $G \to G/N$.
  • Let $\sim$ be the congruence relation defined by $N$; i.e. $x \sim y$ if and only if $xy^{-1} \in N$.

The first key fact is

$$ \pi(S) = (SN) / N $$

where $\pi(S)$ means $\{ \pi(s) \mid s \in S \}$. You can think of $SN$ as the subgroup of everything in $G$ that is congruent (by $\sim$) to an element of $S$.

The second isomorphism theorem states that the right hand side is well defined:

  • $SN$ is a subgroup of $G$
  • $N$ is a normal subgroup of $SN$

The second key fact is that $\sim$ is a congruence relation on $S$, and $S \cap N$ is the congruence class of zero. So you have

$$ S /{ \sim} = S / (S \cap N) $$

where the notation on the left means to take the quotient of $S$ by the congruence relation $\sim$; i.e. it's the set of congruence classes, as usual. The second isomorphism theorem states that this is well defined too:

  • $S \cap N$ is a normal subgroup of $S$

Finally, the second isomorphism theorem states

$$ \pi(S) \cong S / {\sim} $$

With our interpretations of the two sides, we can easily see this as an application of the first isomorphism theorem.