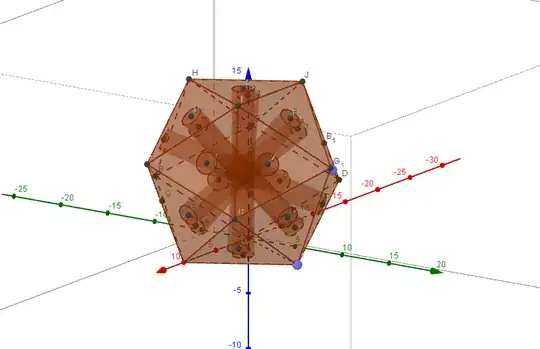
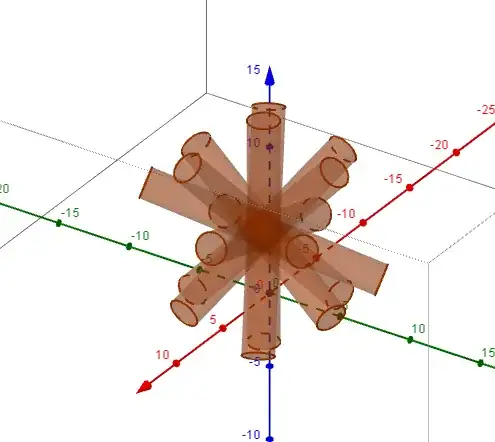
The picture below illustrates what one will get if one intersect ten infinite long cylinders of unit radius, whose axes are aligned along the ten diagonals of a dodecahedron, against each other.
$\hspace1in$
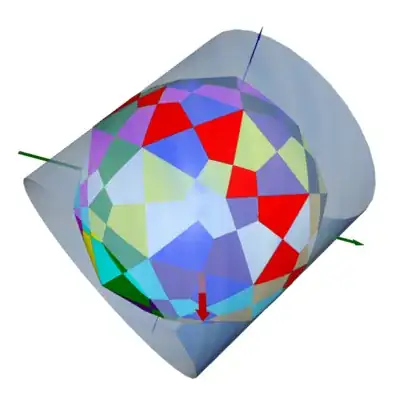
The resulting figure is very complicated.
It consists of $180$ quadrilateral faces and each cylinder contribute $18$ faces.
Faces coming from same cylinder has been colored with same color. For example,
all the red faces lie on a cylinder whose axis is pointing along the $(-1,1,1)$ direction. The $18$ faces from any cylinder fall into two groups. Up to mirror reflection, $12$ of them are congruent to each other. The remaining $6$ faces are congruent to each other directly.
If one study the figure carefully, one will notice the quadrilaterals arrange themselves into $12$ pentagons. Each pentagon carries $15$ quadrilaterals and these pentagons forming the faces of a dodecahedron. As a "dodecahedron", one vertex $U$ of it is lying along the direction $(-1,1,1)$ and another nearby one $V$ is lying along the direction $(0,\phi, \phi^{-1})$ where $\phi$ is the golden ratio.
To simplify analysis, choose a new coordinate system such that $U$ lies along the $z$-axis and $V$ in the $yz$-plane. i.e.
$$\begin{array}{rcl}
(x,y,z)_U^{old} = \sqrt{\frac38} (-1,1,1)
&\mapsto&
(x,y,z)_U = \frac{3}{\sqrt{8}}(0,0,1)\\
(x,y,z)_V^{old} = \sqrt{\frac38} ( 0,\phi,\phi^{-1})
&\mapsto&
(x,y,z)_V = \frac{3}{\sqrt{8}}(0,\frac23,\frac{\sqrt{5}}{3})\\
\end{array}
$$
If one "zoom in" the figure from the direction of new +ve $x$-axis and perform
an orthographic projection to the new $yz$-plane, one see something like below:
$\hspace1in$ 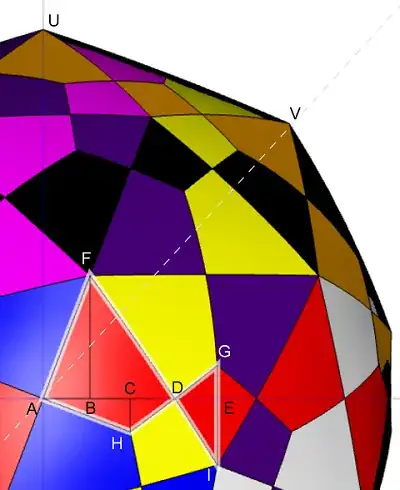
The $18$ red faces now lies along the equator. The cylinder holding them
becomes $$\mathcal{C} \stackrel{def}{=} \{ (x,y,z) : x^2 + y^2 = 1 \}.$$ Furthermore, the $18$ red faces can be viewed as the union of $12$ non-simple polygons. Each of them is congruent to either the non-simple polygon $\mathcal{P}$
with vertices $AHDIGDF$ (the one highlighted by a white border) or its mirror image.
To compute the volume of the intersection, we first need to figure out the
area of $\mathcal{P}$. As shown in figure above, we can break $\mathcal{P}$
into $6$ right angled triangles:
$$\mathcal{P} = \triangle ABF \cup \triangle BDF \cup \triangle AHC \cup \triangle HDC \cup \triangle DEG \cup \triangle DIE$$
It turns out it is not that hard to compute the area of these sort of right angled triangle on a cylindrical surface. Let me use $\triangle ABF$ on $\mathcal{C}$ as an example.
First, the curve $AF$ lies on the intersection of two cylinders. The axes of
these two cylinders are pointing along the direction $OU$ and $OV$ respectively
($O = (0,0,0)$ is the origin, right behind $A$ in above figure).
From above figure, it is easy to see $AF$ lies on the plane equal distance between $U$ and $V$. Let $\alpha = \angle BAF$ and $\beta = \angle VOU$. The slope of $AF$ with respect to the equator is then given by
$$\tan\alpha = \cot\frac{\beta}{2} = \frac{1+\cos\beta}{\sin\beta} =
\sqrt{\frac{1 + \cos\beta}{1 - \cos\beta}} = \sqrt{\frac{3+\sqrt{5}}{3-\sqrt{5}}} = \frac{3+\sqrt{5}}{2} = \phi^2$$
The point $F$ is one of the vertex of the dodecahedra, it is not hard to see $\;z_F = \frac{3}{\sqrt{8}}\cdot \frac13 = \frac{1}{\sqrt{8}}$.
We can parametrize $AF$ by the map $$ [0,\theta_F] \ni \theta\; \mapsto\; (x,y,z) = (\cos\theta,\sin\theta,\tan\alpha\sin\theta ) \in \mathcal{C}
\quad\text{ where }\quad
\tan\alpha\sin\theta_F = z_F
$$
With this parametrization, the area of the $\triangle ABF$ on $\mathcal{C}$ is given by:
$$\int_0^{\theta_F} \tan\alpha \sin\theta d\theta
= \tan\alpha - \tan\alpha \cos\theta_F
= \tan\alpha - \sqrt{\tan\alpha^2 - z_F^2}
= \phi^2 - \sqrt{\phi^4 - \frac18 }
$$
As one can see from this example, given the slope $k$ and height $h$ of
such a right angled triangle, its area on the cylinder can
be computed using following function:
$$A(k,h) = k - \sqrt{k^2 - h^2}$$
Since we are dealing with cylinders with unit radius, the volume of the cone span by $O$ and such a right angled triangle is simply $\frac13 A(k,h)$.
By brute force, one can work out the slopes and heights of remaining $5$ right angled triangles.
To summarize, we have:
$$
\begin{cases}
\tan\angle BAF = \phi^2,\\
\tan\angle HAB = \frac{1}{\phi^2},\\
\tan\angle FDB = \tan\angle IDE = \sqrt{2},\\
\tan\angle CDH = \tan\angle EDG = \frac{1}{\sqrt{2}}
\end{cases}
\quad\text{ and }\quad
\begin{cases}
|z_F| = \frac{1}{\sqrt{8}},\\
|z_G| = |z_H| = \frac{1}{4\phi^2}\\
|z_I| = \frac{1}{2\phi^2}
\end{cases}
$$
From this, we find the volume of the intersection is given by
$$\verb/Volume/ =
\frac{10 \times 12}{3}\left[
\begin{align}
& A\left(\phi^2,\frac{1}{\sqrt{8}}\right)
+ A\left(\sqrt{2},\frac{1}{\sqrt{8}}\right)
+ A\left(\frac{1}{\phi^2},\frac{1}{4\phi^2}\right)\\
+ & 2 A\left(\frac{1}{\sqrt{2}},\frac{1}{4\phi^2}\right)
+ A\left(\sqrt{2},\frac{1}{2\phi^2}\right)
\end{align}
\right]
$$
With help of a CAS, one can simplify this to
$$\begin{align}
\verb/Volume/ &= 5\left(24 + 24 \sqrt{2} + \sqrt{3} - 4\sqrt{6} - 7\sqrt{15} - 4\sqrt{30}\right)\\
&\approx 4.277158048659416687225951566030890254054503016349939576882...
\end{align}
$$ which is about $2\%$ larger than the volume of unit sphere.