2

From what I remember from a lecture I had of a course I'm attending called "introduction to computational science", floating-point numbers are distributed logarithmically. What does it mean? And how can I visualize it?

I've a slide where it is said:

We assume that all binary numbers are normalized. Between powers of 2, the floating point numbers are equidistant.

I think this is related to the logarithmic distribution or spacing of the floating point numbers, but I don't understand exactly what it means.

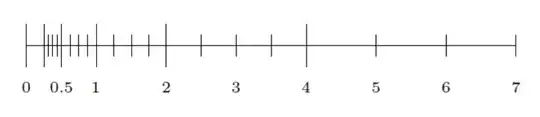
I've also below the statement taken from the same slide this picture:

enter image description here

Apart from the range between $0$ and $0.25$, it seems that the number or density of floating point numbers is decreasing, if this picture actually represents the distribution of floating-point numbers.

Why is that?

Why there's this exception between $0$ and $0.25$?

Community
  • 1

1 Answers1

3

This statement is referring to the fact that there are the same number of floating point numbers representable between $1$ and $2$ as between $2^k$ and $2^{k+1}$ for any $k$. This is because the mantissa of $x$ and $2x$ have the same representation as a floating point number, only the exponent of $2$ changes.

robjohn
  • 353,833
  • Indeed. They are the range from $2^k$ to $2^{k+1}$ for $k=0$. – robjohn Apr 09 '16 at 14:30
  • 1
    There are $3$ ticks between $0.25$ and $0.5$; $3$ ticks between $0.5$ and $1$; $3$ ticks between $1$ and $2$; $3$ ticks between $2$ and $4$; $3$ ticks between $4$ and $8$; etc. It looks logarithmic. – robjohn Apr 10 '16 at 13:13
  • 1
    How many do you think there would need to be between $0$ and $0.25$? One has to stop somewhere before infinity. Sort of like double precision numbers stop at $2^{-1022}$. – robjohn Apr 10 '16 at 13:40