Need to find a 95% confidence interval for $E(Z)$ where $Z=X-Y$ using both paired t-test and Welch's t-test. For one what is the main difference between them and for two how do you do it? Need help studying for a test so the answer can be generic.
-
The best strategy is for you to look at the relevant sections of your text to make sure you know and understand the formulas. I have given an outline of the two situations, emphasizing what I view as important differences between them. So I hope my answer will focus your attention on key features of both kinds of tests, so you don't overlook anything of crucial importance as you study. (As always with material that has so much notation, please double-check all formulas with your text, just to be sure there are no typos.) – BruceET Apr 08 '16 at 04:58
1 Answers
Paired t. Here is the experiment: $n = 50$ subjects take a pre-test on a topic (scores $X_i$), then a class to improve knowledge of the topic, finally a post-test on the topic (scored $Y_i$). Thus difference $D_i = Y_i - X_i$ measures the improvement of the $i$th subject. More capable subjects may score higher on both, less capable subjects lower on both. But all may benefit from the class. However, there is a chance that the course may confuse some students, causing the second test to be lower in some cases. Thus the alternative hypothesis is two-sided.
We wish to test $H_0: \mu_D = 0$ against $H_a: \mu_D \ne 0.$ Where $\mu_D$ is the mean improvement of people in the population from which the subjects are randomly sampled.
Let $\bar D$ denote the sample mean of the $n$ differences $D_i$ and $S_D$ the sample SD. The test statistic is $$T = \frac{\bar D}{S_D/\sqrt{n}}.$$ Under $H_0$ the statistic $T$ has Student's t distribution with $n - 1 = 50 - 1 = 49$ degrees of freedom. Reject $H_0$ at the 5% level of significance if if $|T| > 2.01.$
A 95% confidence interval for $\mu_D$ is $\bar D \pm 2.01 S_D/\sqrt{n}.$
Example: Here are the data from the first 10 of 50 subjects.
i 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00
x 121.57 114.02 100.39 98.11 92.82 119.38 96.21 80.02 121.12 81.43
y 165.96 159.59 143.61 116.56 128.64 186.26 100.60 86.52 165.18 138.29
d 44.39 45.57 43.22 18.45 35.82 66.88 4.39 6.50 44.06 56.86
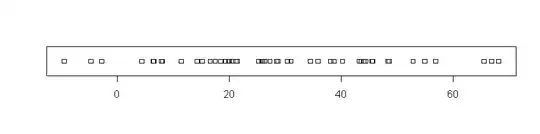
Here is a stripchart of the 50 differences (only three subjects did worse on the post-test than on the pre-test).
Here is output of the test and the CI from R:
mean(d); sd(d)
## 28.4764
## 18.72362
Paired t-test
data: y and x
t = 10.7543, df = 49, p-value = 1.704e-14
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
23.15521 33.79759
sample estimates:
mean of the differences
28.4764
Welch, two-sample separate-variances test. Here is the experiment. City A has a special 9th grade program to teach colonial American history. In City B this subject matter is part of the regular 9th grade history course. We sample $n_1 = 70$ subjects from City A, and $n_2 = 75$ subjects from City B. All are 9th graders who have finished their history topics. All $n_1 + n_2$ subjects are given the same test on colonial American history. We want to know if students in the two cities know significantly different amounts about the topic, as measured by the exam.
We wish to test $H_0: \mu_A = \mu_B$ against $H_a: \mu_A \ne \mu_B$. There is no reason to expect that the population variances $\sigma_A^2$ and $\sigma_B^2$ are necessarily equal.
The test statistic is $$T^\prime = \frac{\bar X_A - \bar X_B}{\sqrt{S_A^2/n_1 + S_B^2/n_2}},$$ where $\bar X_A$ and $\bar X_B$ are the mean test scores for students from the two cities, and $S_A^2$ and $S_B^2$ are the variances of the test scores.
Under the null hypothesis the test statistic $T^\prime$ is approximately distributed as Student's t distribution with degrees of freedom $\nu$ computed according to a formula you will find in your text. Notice that $\min(n_1 - 1, n_2 - 1) = 69 \le \nu \le n_1 + n_2 - 2 = 143.$ Thus $H_0$ is rejected at the 5% level of significance if $|T^\prime| \ge 2.0$ (approximately).
A 95% confidence interval for $\mu_A - \mu_B$ is $(\bar X_A - \bar X_B) \pm 2.0 \sqrt{S_A^2/n_1 + S_B^2/n_2}.$
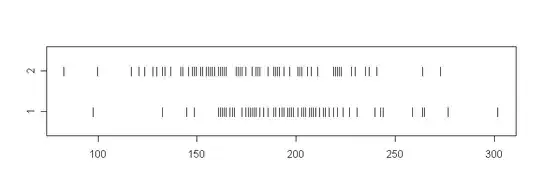
Example: Stripchart of the data. City A (1) scores seem a little higher.
Here is output from the test and CIs.
mean(a); var(a)
## 198.3571
## 1122.233
mean(b); var(b)
## 176.1467
## 1411.316
Welch Two Sample t-test
data: a and b
t = 3.7624, df = 142.711, p-value = 0.0002450
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
10.54118 33.87977
sample estimates:
mean of x mean of y
198.3571 176.1467
Notes on simulated data for the examples: For the paired test, the population differences had mean 30, SD 20; corr(x,y) .52. For the two-sample test, City A had population mean 200, SD 30. Independently, City B had population mean 180, SD 40.
- 52,418
-
Very complete answer, even if I'm more into algebra, I could understand it easily thanks to its clarity, thank you! May I ask how you compute the threshold to obtain the desired level of significance? I mean, do you simply look the rejection values $|T|>2.01$ and $|T'|>2.0$ in a table? I've found a table of t-values on Wikipedia, but was not really satisfied with it: what if I have a sample size of 3000, for instance? Does it mean I have 2999 degrees of freedom and approximate it to the infinity and so simply use 1.960 as a threshold for my t-value at 95% confidence? – Lery Jan 19 '17 at 21:05
-
Yes, for a 95% CI based on large $n$ use 1.96. The t table doesn't print values for very large degrees of freedom because they are very close to corresponding values for standard normal. – BruceET Jan 19 '17 at 22:38