13

Edit - I changed the title and much of the body to better reflect my full question. The old one I don't really care about, although I appreciate Fabian's answer of course.

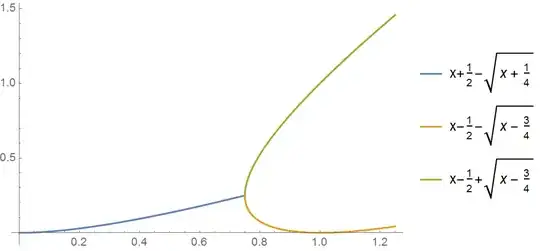
Here is the plot for the function (or map), defined as follows:

$$f_0(x)=x^2$$

$$f_n(x)=(x-f_{n-1}(x))^2$$

If the limit exists, then:

$$f(x)=\lim_{n \to \infty} f_n(x)$$

If the map oscillates between two or more (finite number) of states, I define several limits.

$$0<x<\frac{3}{4}$$

$$f(x)=x+\frac{1}{2}-\sqrt{x+\frac{1}{4}}$$

$$\frac{3}{4}<x<\frac{5}{4}$$

$$f_{a}(x)=x-\frac{1}{2}-\sqrt{x-\frac{3}{4}}$$

$$f_{b}(x)=x-\frac{1}{2}+\sqrt{x-\frac{3}{4}}$$

Then the function splits into four branches, and soon (for $x \in (1.36,1.37)$ ) splits again and later becomes chaotic.

However, there is a special value:

$$f(2)=4$$

enter image description here

So, the most important question - how to completely describe and prove the properties of this map in the range $0<x<2$?

For larger $x$ the function becomes infinite.

Edit

I found some sources on this map, for example this one

This is what the map looks like if we don't square on the last step:

enter image description here

Actually, most of my question is answered in the linked paper.

Another (professional) paper on this map is here. Mathworld entry is quite extensive as well.

Here is the old question.

For any $|x|<1$ we can expand the square root in the following way:

$$\sqrt{1+x}=1+\frac{x}{2}-2\left(\frac{x}{4}-\left(\frac{x}{4}-\left(\frac{x}{4}- \dots \right)^2 \right)^2 \right)^2$$

Turns out the above formula is valid for all $0<x<3$.

How does this quadratic map manage to give the correct values for the root when the Taylor expansion fails?

This one, on the other hand works only for $|x|<1$:

$$\sqrt{1-x}=1-\frac{x}{2}-2\left(\frac{x}{4}+\left(\frac{x}{4}+\left(\frac{x}{4}+ \dots \right)^2 \right)^2 \right)^2$$

Still, this formula is much more convenient than the Taylor series, because there is no need to remember (or derive) the coefficients for each term.

Moreover, we can create very good (arbitrarily accurate) infinite expansions for square roots, for example:

$$\sqrt{2}=\frac{3}{2}-4\left(\frac{1}{8}+\left(\frac{1}{8}+\left(\frac{1}{8}+ \dots \right)^2 \right)^2 \right)^2$$

$$\sqrt{3}=\frac{7}{4}-4\left(\frac{1}{16}+\left(\frac{1}{16}+\left(\frac{1}{16}+ \dots \right)^2 \right)^2 \right)^2$$

Community
  • 1
Yuriy S
  • 32,728
  • 2
    "This formula is much more convenient than the Taylor series, because there is no need to remember the coefficients for each term" : very funny, lol. – reuns Apr 07 '16 at 11:53
  • @user1952009, I know that coefficients are computed by binomial coefficients for $1/2$, or directly by derivatives, but it's not an easy computation – Yuriy S Apr 07 '16 at 11:54
  • 2
    you can see when writing it that you can't find any rigorous meaning to that : what is "easy" ? the speed of convergence ? the number of lines of codes needed by a program computing the function to an arbitrary precision ? – reuns Apr 07 '16 at 11:58
  • Maybe it's just me, but I don't understand what in the world this question is asking: what do you mean by redefining $f$ piecewise if it oscillates, and what was the purpose of taking the limit of the original recursion (since your graph only shows the piecewise definitions)? – Pockets Apr 17 '16 at 07:14
  • @Pockets, I've found most of the answers in the links I provided right after setting the bounty. So the question is kind of pointless now. – Yuriy S Apr 17 '16 at 09:07

1 Answers1

7

It looks closely related to Newton's way to compute the square-root. If you want the square root of $1+x$, you generate the sequence $$a_{n+1}= \frac12\left(a_n + \frac{1+x}{a_n}\right)$$ with $a_0$ some initial guess. You can show that $\sqrt{1+x} = \lim_{n\to\infty} a_n$.

Your method on the other hand is obtained from the sequence $$ b_{n+1} = \left(\frac{x}4 - b_n \right)^2.$$ You can show that $\lim_{n\to\infty}(2 b_n) = 1+ \frac12 x - \sqrt{1+x}$, for proper initial conditions.

Fabian
  • 24,230
  • @YuriyS : if you have some derivation of your formula, why don't you write it ... ? your question as it is means : "do you have a proof that my formula is valid" – reuns Apr 07 '16 at 12:00
  • @YuriyS: I don't think it has a name. I can produce (infinitely) many series that converge to the squareroot of some number. I just wanted to point out that the general idea is the same as Newton's method. Newton's method has a name as it always converges (fast), you also don't have to remember coefficients of some Taylor series. Thus, it is in many ways better than your series (and thus the series has a name). – Fabian Apr 07 '16 at 12:07
  • FYI.For computing $ A^{1/k}$ for $2\leq k\in N$ and $A>0$, let $0<x_1$ and let $x_{n+1}=x_n+2 x_n(A-(x_n)^k)/D_n$ where $D_n=(k+1)(x_n)^k+(k-1)A$. This approximately triples the number of digits of accuracy with each step. – DanielWainfleet Apr 07 '16 at 13:02