7

I had looked around on the web and can't find much information related to the integration of piecewise continuous functions.

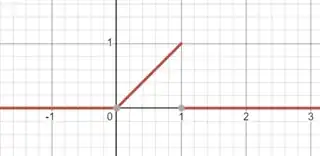
Let's say we have a simple function

$$f(x)= \begin{cases} 0 & x\leq 0 \\ x & 0\leq x\leq 1 \\ 0 & x>1 \end{cases}$$

and we are looking to find the integral $\int f(x) dx$

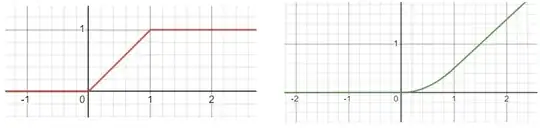
WolframAlpha gives me the following result:

$$\int f(x) dx= \begin{cases} c & x\leq 0 \\ \frac{x^2}{2}+c & 0\leq x\leq 1 \\ \frac{1}{2}+c & x>1 \end{cases}$$

The cases $x\leq 0$ and $0\leq x\leq 1$ are clear. But why do we need the $\frac{1}{2}$ for the $x>1$ case? I see that this makes the integral continuous but is it necessary, i.e. is it wrong to have simply $c$ for the $x>1$ case for the integral?

ryang
  • 44,428
user328855
  • 73
  • 1
  • 4
  • 1
    Maybe the reason is that if you want to calculate $\int_a^b f(x),dx$ with $b>1$ you can just insert the upper limit, and it will be correct. – mickep Apr 06 '16 at 05:55
  • But $\int_a^b f(x) dx$ with $b>1$ evaluates to just $\int_a^1 f(x) dx$ doesn't it? So there is no difference whether you have the $\frac{1}{2}$ or not. – user328855 Apr 06 '16 at 06:19
  • Well, yes, but since the $1/2$ is there, one could equally well think of it as inserting the upper limit at $x=b$ instead of $x=1$, in the spirit of $\int_a^bf(x),dx=F(b)-F(a)$ where $F$ is a primitive of $f$. – mickep Apr 06 '16 at 06:23
  • There is a reason why they are called INDEFINITE integrals! – user310540 Apr 06 '16 at 06:25
  • 1
    Actually, you say that it is clear for $x\leq 0$, but it is really the same thing happening there. Why choose $c$ and not $3+c$ or $-4+c$? It is choosen so that you get continuity at $x=0$. Again, it fits well with $\int_a^b f(x),dx$ with $a<0$. – mickep Apr 06 '16 at 06:26

3 Answers3

4

The short answer is no. An indefinite integral is not a continuous function, because an indefinite integral is not a function. However, once you fix $a\in \mathbb{R}$, $$\int_a^x f(t)dt$$ is a continuous function. Note that once we fix $a$, the constant of integration is completely determined.

user310540
  • 448
0

Actually, the indefinite integral of a continuous function is a family of continuous functions. If you want to find exactly one of these functions, you have to fix an initial condition $F(x_0) = C_0$.

If you want to obtain the same function obtained by WolframAlpha, solve for the following equalities: lateral limits

PythonSage
  • 1,072
Rafael Marcel Asmat Uceda
  • 1
0

$$f(x)= \begin{cases} 0 & x< 0 \\ x & 0\leq x\leq 1 \\ 0 & x>1 \end{cases}$$ enter image description here

WolframAlpha gives me the following result: $$\int f(x) \,\mathrm dx= \begin{cases} C & x< 0 \\ \frac{1}{2}x^2+C & 0\leq x\leq 1 \\ \frac{1}{2}+C & x>1 \end{cases}$$

$f$ has a jump discontinuity at $1,$ so has no antiderivative at $1,$ so has no indefinite integral (its complete set of antiderivatives), so Wolfram's result is technically incorrect.

However, for $$g(x)= \begin{cases} 0 & x< 0 \\ x & 0\leq x\leq 1 \\ \color{brown}1 & x>1 \end{cases},$$ enter image description here

we do have $$\int g(x) \,\mathrm dx= \begin{cases} C & x< 0 \\ \frac{1}{2}x^2+C & 0\leq x\leq 1 \\ \color{brown}{x-\frac{1}{2}+C} & x>1 \end{cases}.$$

why do we need the $\frac{1}{2}$ for the $(x>1)$ case? I see that this makes the integral continuous but is it necessary ?

Every antiderivative is by definition differentiable, and thus continuous. In other words, every instantiation of (i.e., for each value of $C$) every indefinite integral must be continuous. (Therefore, for each antiderivative with an interval domain, the vertical shifts of its various pieces depend on one another; here, adjusting the $(x>1)$ case by -½ ensures that the antiderivatives are continuous.)

ryang
  • 44,428