13

Question: Can a disc drawn in the Euclidean plane be mapped to the surface of a hemisphere in Euclidean space ?

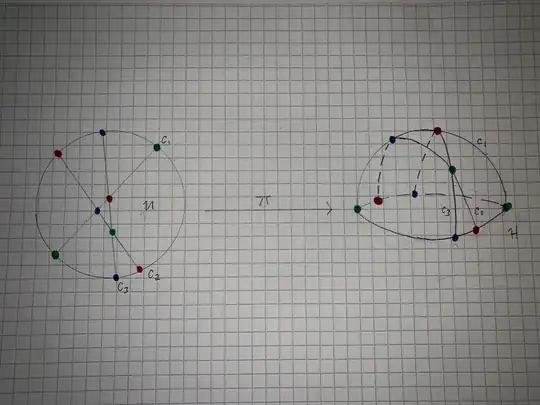
If $U$ is the unit disc drawn in the Euclidean plane is there a map, $\pi$, which sends the points of $U$ to the surface of a hemisphere, $H,$ in Euclidean space ?

Background and Motivation:

If $U$ is the unit disc centered at the origin consider $n$ chords drawn through the interior of $U$ such that no two chords are parallel and no three chords intersect at the same point. The arrangement graph $G$ induced by the discs and the chords has a vertex for each intersection point in the interior of $U$ and $2$ vertices for each chord incident to the boundary of $U.$ Naturally $G$ has an edge for each arc directly connecting two intersection points. $G$ is planar and $3-$connected. I know that $G$ has $n(n+3)/2, n(n+2)$ and $(n^2+n+4)/2$ vertices, edges and faces respectively. That $G$ is Hamiltonian-connected follows from R. Thomas and his work on Plummer's conjecture. I have conjectured that $G$ is $3-$colourable and $3-$choosable.

Independently Felsner, Hurtado, Noy and Streinu :Hamiltonicity and Colorings of Arrangement Graphs, ask if the arrangement graph of great circles on the sphere is $3-$colourable. In addition they conjecture such an arrangement is $3-$choosable.

Now I began to think the following

  1. Show my graph $G$ is $3-$colourable
  2. $\pi:G \to H$
  3. Glue $H$ to a copy of itself at the equator

then I could solve the conjecture by Felsner and his colleagues. Moreover if the map $\pi$ is bijective then any solution to Felsner's conjecture will also solve mine. The map $\pi$ does not need to preserve angles or surface areas. $\pi$ necessarily will have to map chords to great circles. See @JohnHughes excellent answer concerning the map $\pi$ and why vertical projection will not work.

enter image description here

Anthony
  • 4,078
  • 16
  • 35

3 Answers3

21

If by a "circle" you mean the set of all points inside a circle (e.g., points whose distance from some center $C$ is less than or equal to 1), then the answer is "yes" and one solution is called "stereographic projection;" another is "vertical projection".

If you have a point $(x, y)$ in the unit disk (the "filled in circle"), the corresponding point, using vertical projection, is $(x, y, \sqrt{1 - x^2 - y^2})$.

For stereographic projection, you send the point $P = (x, y)$ to a new point $Q$: \begin{align} h &= x^2 + y^2 \\ Q &= (\frac{x}{h+1}, \frac{y}{h+1}, \frac{h-1}{h+1}) \end{align}

The latter has the charm that it takes chords in your disk to great-circle arcs in the hemisphere, and preserves angles of intersection, although not lengths.

John Hughes
  • 100,827
  • 4
  • 86
  • 159
  • I thought Stereographic Projection required the "whole" sphere. – Anthony Apr 05 '16 at 14:50
  • 3
    Stereographic projection from the north pole $(0,0,1)$ of a unit sphere whose equator is on the $xy$-plane will take points in the lower hemisphere to those within the unit disk in the plane, and points in the upper hemisphere to those outside the unit disk. So the map I've given you will send points of your disk (for which $h < 1$) to points in the southern hemisphere (for which $z < 0$), as you can see by noting that $h + 1$ is positive, but $h-1$ is negative. – John Hughes Apr 05 '16 at 15:02
  • I can then "glue' together two copies of the same blown up hemisphere $H +_{glue} H$ to get an arrangement of great circles on the sphere - assuming we lined them up correctly? – Anthony Apr 05 '16 at 15:08
  • I'm not certain I understand your question. You can certainly change $\frac{h-1}{h+1}$ to $-\frac{h-1}{h+1}$ to get a map from the disk to the NORTHern hemisphere. If you take an arrangement of $k$ segments in the disk and perform both mappings, you'll get $2k$ circle-arcs on the sphere that way...but they won't join nicely (i.e., a single disk-segment will lift to two arcs, but they will not generally be arcs of the same great circle). – John Hughes Apr 05 '16 at 16:25
  • Keep it straightforward draw a line across the circle. Blow it up to the hemisphere. Now make a copy of that. You now have two hemispheres and each one has an arc going across it. Now take both copies and glue them so that both ends of the arc match up along the equator (or base) of the hemisphere? – Anthony Apr 05 '16 at 17:12
  • 1
    If by "blow it up" you mean "project vertically," then you'll end up with a circle on the sphere if you do what you've described. But it won't in general be a great circle (unless your initial line segment is a diameter of the disk), and the angles between segments will not be preserved as they are when you use stereographic projection. – John Hughes Apr 05 '16 at 17:56
  • I do not need the circles to be great. I only need the point line incidence to be preserved. – Anthony Apr 05 '16 at 18:52
  • 1
    OK...then any bijection at all will do. But for others who might care about that, I'm gonna leave it in my answer. :) – John Hughes Apr 05 '16 at 22:20
  • Actually not any bijection will do? A vertical projection might introduce a lune and consequently not preserve the point-line incidence relation of the chords drawn across the circle. This might be the case if no chords are parallel over the unit disc. – Anthony Apr 06 '16 at 12:46
  • 1
    If two arcs (not necessarily circular -- any nice image of a closed interval will do) on the hemisphere intersect, then their images, under any bijection with the disk, intersect in the disk, and vice versa. Indeed $f(A \cap B) = f(A) \cap f(B)$ for any bijection $f$ and any two subsets of $f$'s domain. – John Hughes Apr 06 '16 at 14:59
9

I think you mean to say disk instead of circle.

If you mean disk then you can do it.

Just imagine of punching the disk from center, it will give you a hemisphere.

And if you want precisely the map then you can get it from Stereographic projection.

EDIT

It will look something like this when you punch a disk.

enter image description here

User
  • 2,966
2

Projecting the hemisphere onto the circle bounded by the equator from a point infinitely far above the North pole maps the hemisphere bijectively to the circle. Take the inverse of this map.

Ethan Bolker
  • 103,433