$X

Question

$\newcommand{\avar}{\mathrm{AV@R}_{\alpha}} \renewcommand{\Re}{\mathbb{R}}$Let $(\Omega, \mathscr{F}, \mathrm{P})$ be a probability space and define $\mathcal{Z}:=\mathcal{L}_p(\Omega, \mathscr{F}, \mathrm{P})$ for some $p\in [1,\infty)$.

The average value-at-risk of a $X\in\mathcal{Z}$ - often referred to as expected shotfall or conditional value-at-risk is defined as

$$ \avar[X] := \inf_{t\in\Re}\{t+\alpha^{-1}\mathbb{E}[(X-t)_+]\}, $$

where $\mathbb{E}$ is the expectation operator and $(\cdot)_+$ is defined as $(Z)_+=\max\{0, Z\}$.

There are a few other useful formulae. For example

$$ \avar[X] = \mathbb{E}[X\mid X\geq \Phi_X^{-1}(1-\alpha)], $$

where $\Phi_X^{-1}$ is the inverse cumulative distribution function of $X$, and, the dual representation

$$ \avar[X] = \sup_{\zeta\in\mathfrak{A}}\langle \zeta, X\rangle $$ where $\langle \zeta, X\rangle:=\int_{\Omega}\zeta X \mathrm{dP}$ and $\mathfrak{A}:=\left\{\zeta\in \mathcal{L}_q(\Omega,\mathscr{F},\mathrm{P}) \mid \mathbb{E}[\zeta]=1, \zeta\in[0,\alpha^{-1}]\ \text{a.s.}\right\}$.

Given that $X\leq Y$ almost surely we know that $\avar[X]\leq \avar[Y]$ by the monotonicity property of $\mathrm{AV@R}[\cdot]$. However, I I believe it is not true that $\avar[X]< \avar[Y]$ whenever $X<Y$ (a.s.).

My question. I suspect that this assertion is false, but I would like to find a counterexample.

My guess. If we take $X<Y$ (a.s.) then, since all $\zeta\in\mathfrak{A}$ are nonnegative (a.s.), we have $\langle \zeta, X\rangle \leq \langle \zeta, Y\rangle $ from which we can infer $\avar[X]\leq \avar[Y]$, but not $\avar[X]<\avar[Y]$.

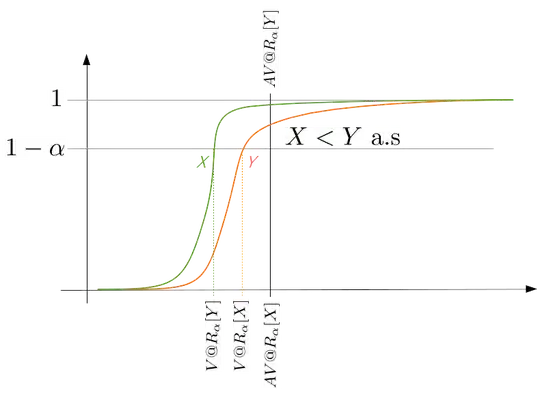
Intuition. In order to acquire some intuition about this problem, I create the figure below.

The CDFs of the two variables don't have the same shape, they have different value-at-risk values, but the same average value-at-risk, it is $X<Y$. The CDF of $X$ after its value-at-risk moves faster to $1$ and as a result its average value-at-risk is further away from its value-at-risk. On the other hand, the CDF of $Y$ exhibits a more sluggish ascend and the two AV@Rs coincide.

Answer 1

$\newcommand{\avar}{\mathrm{AV@R}_{\alpha}} \newcommand{\var}{\mathrm{V@R}_{\alpha}}$I figured out that my guess was wrong: $\avar$ is strictly monotone, but not strongly monotone. Let us give the definitions:

A risk measure $\rho:\mathcal{Z}\to\Re$ is strictly monotone if $\rho(X)<\rho(Y)$ whenever $X<Y$ (a.s.).

A risk measure $\rho:\mathcal{Z}\to\Re$ is strongly monotone if $\rho(X)<\rho(Y)$ whenever $X\leq Y$ (a.s.) and $P(X<Y)>0$.

$\avar$ for $\alpha\in[0,1)$ is strictly monotone because

$$ \begin{align*} \avar[X]&=\mathbb{E}[X\mid X\geq \var[X]]\\ &= \int_{\var[X]}^{+\infty}X\mathrm{dP}\\ &< \int_{\var[X]}^{+\infty}Y\mathrm{dP}\\ &\leq \int_{\var[Y]}^{+\infty}Y\mathrm{dP}\\ &= \avar[Y] \end{align*} $$

The strict inequality above is because of the strict monotonicity property of the integral and the second inequality is because $X<Y$ (a.s.) implies $\var[X]\leq \var[Y]$.

Now note that $\mathrm{AV@R}_0[\cdot]=\mathbb{E}[\cdot]$ by convention; this is because $\avar[X]=\mathbb{E}[X\mid X\geq \var[X]]$ and $\mathrm{V@R}_{0}[X]=\mathrm{esssup}[X]=\|X\|_{\infty}$. Take $X,Y\in\mathcal{L}_{\infty}(\Omega, \mathscr{F}, \mathrm{P})$ such that $X<Y$ (a.s.). Then $X\leq Y$ (a.s.). In that case, however, we may have $X<Y$ and $\|X\|_{\infty}=\|Y\|_{\infty}$; take for instance $\mathcal{Z}=\mathcal{L}_{\infty}(\Re_+,\mathcal{B}_{\Re_+}, \mathrm{P})$ and

$$ X(\omega)=\frac{\omega}{\sqrt{1+\omega^2}} \text{ and } Y(\omega)=\mathrm{erf}\left(\frac{\sqrt{\pi}}{2}\omega\right) . $$

Finally, it is easy to see that $\avar[\cdot]$ is not strongly monotone and we can easily construct counterexamples using the fact that it does not account for the left tail of the distribution.