You may read [this post] 1, but let me give you a geometric interpretation of decomposing 3-sphere into two solid tori.
The idea is to regard $S^3$ as $\mathbb R^3$ plus a infinity point, and embed one solid torus $\textbf{T}$ into $\mathbb R^3$, and try to think why $(\mathbb R^3\cup {\infty})- \textbf{T}$ corresponds to the other solid torus.
Let's say $\textbf{T}$ is bounded by the torus $$x(u,v)=(3+\cos v)\cos u,\\ y(u,v)=(3+\cos v)\sin u,\\ z(u,v)=\sin v$$
Let me explain the decomposition in the following pictures.
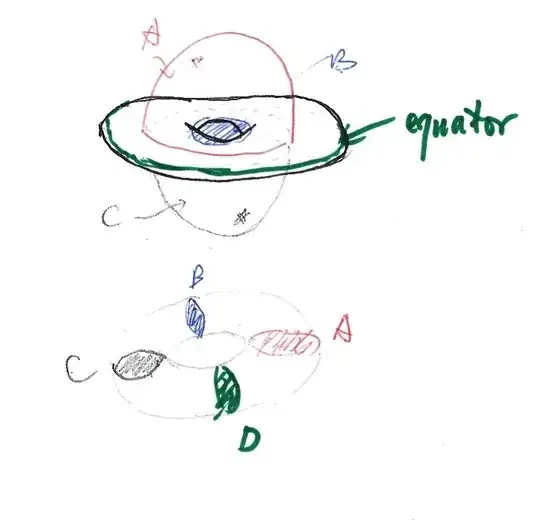
The first picture is some disks attached on $\textbf{T}$, and the second picture show how these disks gives you another solid torus.
As you see in the picture, the boundary of $\textbf{T}$ is a torus drawn in black, and the green circle is its equator. Now pick any meridional circle, say the red loop on torus, you can have a $D^2$ with boundary attached with the circle, e.g., the surface A.
Now, the key point is to regard the upper space $\mathbb R_+^3-\textbf{T}$, i.e, the complement of $\textbf{T}$ with coordinate $z>0$, as slices of disks $(0,1)\times D^2$, with $\{0\}\times D^2$ corresponds to the disk B, and $\{1\}\times D^2$ corresponds to disk D at the equator (we haven't define this disk yet). And you can do the same thing downside for the lower space $\mathbb R_-^3 - \textbf{T}$, which gives you $(-1,0)\times D^2$, with point $\{-1\}\times D^2$ corresponds to disk at equator. Now, Attach them together at point $\{0\}\times D^2$ with disk B in blue color, we get $(-1,1)\times D^2$, and the remaining space is just $\{(x,y,0)|x^2+y^2>9\}\cup \{\infty\}$, but this is just an open disk removed from $S^2$, which is exactly $D^2$, and this gives you the last disk drawn in green color, which corresponds to $\{1\}\times D^2=\{-1\}\times D^2$. (At this point, you should think topologically why the green disk fit in place the second picture!)
Finally, you get a $S^1\times D^2$, which is exactly another solid torus.
