2

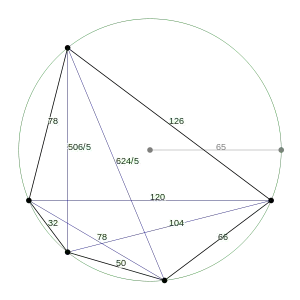
The Heron triangle has integer sides and area. The Robbins pentagon is just the generalization: it also has integer sides and area. The example below has sides $78, 126, 66, 50, 32$ and area $A_R = \color{brown}{4392}$.

$\hskip2.0in$enter image description here

Define the formula for the area of Heron triangles as,

$$A_H(a,b,c) = \frac{1}{4}\sqrt{(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)}$$

We can partition the above Robbins pentagon into three Heron triangles and find that indeed,

$$A_R = A_H(78,126,120) + A_H(32,120,104) + A_H(104,50,66) = \color{brown}{4392}$$

P.S. Notice that the five diagonals form a pentagram (a $5$-pointed star) and also form a small pentagon .

Question:

  1. For this example, what is the area $A_r$ of the small pentagon?
  2. In general, if $A_R$ is rational, then is $A_r$ also rational?
Tito Piezas III
  • 60,745

1 Answers1

2

We can place the large pentagon on a coordinate plane such that the vertices are $$\{(0,0), (96/5, -128/5), (336/5, -198/5), (120,0), (96/5, 378/5)\}.$$

Then the coordinates of the small pentagon $p'$ would be $$\left\{\left(\tfrac{3072}{85}, -\tfrac{12672}{595}\right), \left(\tfrac{10893}{190}, -\tfrac{1512}{95}\right), \left(\tfrac{507}{10}, 0\right), \left(\tfrac{96}{5},0\right), \left(\tfrac{96}{5}, -\tfrac{396}{35}\right)\right\}.$$ The resulting area is $$A_r = \frac{6983658}{11305}.$$

but $p'$ is not a Robbins pentagon.

The answer to your second question is not likely to be known, because it is not yet known whether there exist any Robbins pentagons that have interior diagonals that are irrational, but this is not a rigorous argument by any means.

Tito Piezas III
  • 60,745
heropup
  • 143,828
  • Wow, great! But re my comment above, this would imply a family of Robbins pentagons that are getting infinitely smaller, doesn't it? – Tito Piezas III Feb 17 '16 at 19:30
  • Not necessarily. We do know that if a Robbins pentagon has vertices with rational coordinates, then the intersection of their diagonals will also be rational, but this does not guarantee that the side lengths of the interior pentagon will also be rational. – heropup Feb 17 '16 at 19:35
  • A small favor. Can you find the diagonals of the small Robbins pentagon and see if it yields an even smaller Robbins pentagon? Maybe instead it will have irrational diagonals and you'll find the first example. :) – Tito Piezas III Feb 17 '16 at 19:36
  • That would not help. The small pentagon is not a Robbins pentagon because although its coordinates are rational, its side lengths are not all rational: only two of its sides are rational. – heropup Feb 17 '16 at 19:37
  • Ok, I got it now. The area $A_r$ is rational, but its sides are not. Dang... – Tito Piezas III Feb 17 '16 at 19:39