7

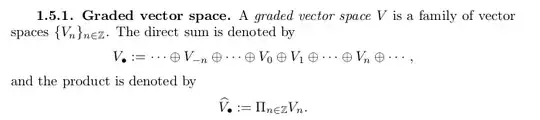
I am studying Algebraic Operads with the book Algebraic Operads, by Jean-Louis Loday and Bruno Vallette and I'm having a little problem with the definition of graded vector space. My advisor and I disagree on the definition. The book defines it this way: enter image description here

my advisor thinks it is equivalent to saying that $V = \bigoplus_{n\in \mathbb{Z}} V_n$. I believe that they are different. In nLab (Graded Vector Spaces) I found the following definition enter image description here

which strengthens my argument. Finally, who is correct? Can anyone suggest me any other reference about graded vector spaces?

Pryscilla Silva
  • 843
  • What does your advisor mean by $\sum_{n \in \mathbb{Z}}V_n$? At the moment, it just seems you are disagreeing on notation (I'm guessing you would write $\oplus_{n\in\mathbb{Z}}V_n$). – Michael Albanese Feb 12 '16 at 12:44
  • Sorry, I typed wrong. I corrected now. – Pryscilla Silva Feb 12 '16 at 12:46
  • I don't understand what notation you are proposing to use for a graded vector space. The one in the first screenshot and the one proposed by your advisor denote the same thing as far as I can tell. – Michael Albanese Feb 12 '16 at 12:51

1 Answers1

8

There are two different categories:

  • The category $\mathsf{gVec}$ where objects are vector spaces $V$ equipped with a decomposition $V \cong \bigoplus_{n \in \mathbb{Z}} V_n$, and morphisms are linear maps respecting the decomposition;
  • The category $\mathsf{Vec}^\mathbb{Z}$ of families of vector spaces $\{ V_n \}_{n \in \mathbb{Z}}$ and morphisms $f : \{V_n\} \to \{W_n\}$ are families of linear maps $\{f_n : V_n \to W_n\}_{n \in \mathbb{Z}}$.

These two categories are equivalent; you can construct an explicit equivalence $\mathsf{Vec}^\mathbb{Z} \to \mathsf{gVec}$ given by $\{V_n\} \mapsto V_\bullet = \bigoplus_{n \in \mathbb{Z}} V_n$. So it makes no difference to consider graded vector spaces from the first point of view or from the second point of view.

Najib Idrissi
  • 56,269