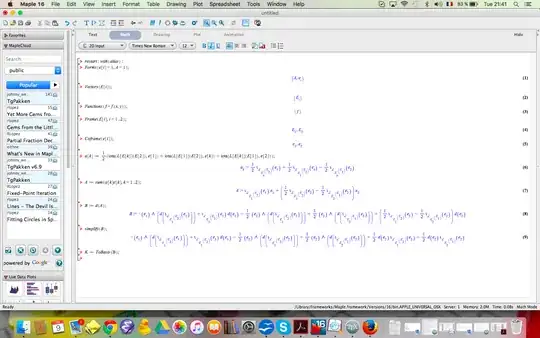
@Paul, I must confess that it is not clear to me exactly what you are looking for in regards to 4.), but I think that what you can do with Atlas combined with a little exterior algebra works quite nicely. (I have attached a screen shot of my Maple file below and I am having some issues with some of the simplifications as well. I seem to remember having these problems before, but of late I have been using Mathematica and a newer version of Atlas. The attached screen shot is from what I believe to be the original version of Atlas and Maple 15 so it is possibly outdated. I apologize for any confusion that this causes.)
Notation: In keeping with the notation of Atlas, I use $\iota$ for the interior product of a vector field with a differential form.
Key Theorems:
- For any differential 1-form $\omega$, $\mathrm{d}\omega$ is defined by
$$
\mathrm{d}\omega\left(X, Y\right) = X\left(\omega\left(Y\right)\right) - Y\left(\omega\left(Y\right)\right) - \omega\left( \left[ X, Y\right]\right),
$$
where $X$ and $Y$ are arbitrary vector fields.
- For any differential form $\omega$ and any vector field $X$, we have the following relationship between the interior product, the Lie derivative, and the exterior derivative
$$ \iota_{X} \mathrm{d}\omega = \mathcal{L}_{X} \omega - \mathrm{d}\left(\iota_{X} \omega\right).$$
- Suppose that $\omega^{i}$ constitute a local coframe with dual frame $E_{i}$. Then
$$\mathcal{L}_{E_{i}}\omega^{j} = A_{ik}^{j}\omega^{k} = - \omega^{j}\left(\left[E_{i}, E_{k}\right]\right)\omega^{k} = -C_{ik}^{j}\omega^{k},$$
where $C_{ik}^{j}$ are the structure functions of the frame $E_{i}$, i.e., $\left[E_{i}, E_{k}\right] = C_{ik}^{j}E_{j}$.
Now, assuming that we are on a two dimensional manifold and that $\omega^{1}$ and $\omega^{2}$ form an orthonormal coframe for a metric tensor $g$, i.e., $g = \omega^{1} \otimes \omega^{1} + \omega^{2} \otimes \omega^{2}$, one calculates $\omega^{1}_{2}$ to be
$$
\omega^{1}_{2} = \frac{1}{2}\left(\,\iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{1}} \right) \right) +
\,\iota_{{E_{{1}}}} \left( \iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{1}} \right) \right) \right) \omega^{{1}}-\,\iota_{{E_{{1}}}}
\left( \mathrm{d} \left( \omega^{{2}} \right) \right) + \,\iota_{{E_{{1}}}}
\left( \iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{2}} \right)
\right) \right) \omega^{{2}}\right).
$$
Going term-by-term through $\omega^{1}_{2}$ we have
$\iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{1}} \right) \right)= \mathcal{L}_{E_{2}}\omega^{1} = -C_{2k}^{1}\omega^{k} = C_{12}^{1}\omega^{1}$
$\iota_{{E_{{1}}}} \left( \iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{1}} \right) \right) \right) \omega^{{1}} = -\omega^{1}\left(\left[E_{2}, E_{1}\right]\right)\omega^{1}= C_{12}^{1}\omega^{1}$
- $-\,\iota_{{E_{{1}}}}
\left( \mathrm{d} \left( \omega^{{2}} \right) \right) = -\mathcal{L}_{E_{1}}\omega^{2} = \omega^{2}\left(\left[E_{1}, E_{k}\right]\right)\omega^{k} = C_{12}^{2}\omega^{2}$
- $\iota_{{E_{{1}}}}
\left( \iota_{{E_{{2}}}} \left( \mathrm{d} \left( \omega^{{2}} \right)
\right) \right) \omega^{{2}} = -\omega^{2}\left(\left[E_{2}, E_{1}\right]\right) \omega^{2} = C_{12}^{2}\omega^{2}.$
We thus have
$$
\omega^{1}_{2} = C_{12}^{1}\omega^{1} + C_{12}^{2}\omega^{2},
$$
and one can see that
$$\mathrm{d}\omega^{1} = -\omega^{1}_{2} \wedge \omega^2 = -C_{12}^{1}\omega^{1} \wedge \omega^{2}.$$
Furthermore, we have
$$\mathrm{d}\omega^{2} = -\omega^{2}_{1} \wedge \omega^1 = \omega^{1}_{2}\wedge \omega^{1} = C_{12}^{2} \omega^{2}\wedge \omega^{1} = -C_{12}^{2}\omega^{1}\wedge\omega^{2}
$$
To calculate the curvature, we now have
\begin{align*}
\mathrm{d}\omega^{1}_{2} &= \mathrm{d}\left(C_{12}^{1}\omega^{1} + C_{12}^{2}\omega^{2}\right)\\
&= \mathrm{d}C_{12}^{1}\wedge \omega^{1} + C_{12}^{1}\mathrm{d}\omega^{1} +\mathrm{d}C_{12}^{2}\wedge\omega^{2} +C_{12}^{2}\mathrm{d}\omega^{2}\\
&= \mathrm{d}C_{12}^{1}\wedge \omega^{1} + C_{12}^{1}\left(-C_{12}^{1}\omega^{1}\wedge \omega^{2}\right) +\mathrm{d}C_{12}^{2}\wedge\omega^{2} +C_{12}^{2}\left(-C_{12}^{2}\omega^{1}\wedge\omega^{2}\right)\\
&= \left(E_{1}C_{12}^{1}\omega^{1} + E_{2}C_{12}^{2}\omega^{2}\right) \wedge \omega^{1} - \left(C_{12}^{1}\right)^2\omega^{1}\wedge \omega^{2} +\left(E_{1}C_{12}^{2}\omega^{1} +E_{2}C_{12}^{2}\omega^{2}\right)\wedge\omega^{2} -\left(C_{12}^{2}\right)^2\omega^{1}\wedge\omega^{2}\\
&=E_{2}C_{12}^{2}\,\omega^{2} \wedge \omega^{1} -\left(C_{12}^{1}\right)^2\left(\omega^{1}\wedge \omega^{2}\right) + E_{1}C_{12}^{2}\omega^{1}\wedge\omega^{2} -\left(C_{12}^{2}\right)^2\omega^{1}\wedge\omega^{2}\\
&= \underbrace{\left(-E_{2}C_{12}^{2} - \left(C_{12}^{1}\right)^2 + E_{1}C_{12}^{2} - \left(C_{12}^{2}\right)^2\right)}_{K}\omega^{1}\wedge \omega^{2}
\end{align*}
Note: In the Maple file created with Atlas, I wrote $\omega^{1}_{2}$ as $$\omega^{1}_{2} = \phi = A \omega^{1} + B \omega^{2}, $$
where $A= C_{12}^{1}$ and $B = C_{12}^{2}$. I also did not spell out explicitly where I used the three key theorems in the substitutions. Let me know if you have any additional questions and/or spot any errors.
I initially thought that there would be a more direct solution using Atlas, but this is the best that I see at the moment.