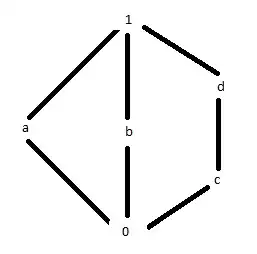
The trivial congruences are $\Delta$, the equivalence relation that only says $x\sim x$ for $x\in\{0,a,b,c,d,1\}$, and $\nabla$, the full relation.
Now let $\theta$ be a congruence, and suppose that $0$ is equivalent to some $x\in\{a,b,c\}$ in the lattice. Then since $0\vee y = y$ for all $y$, and $x\vee y = 1$ for all $y\in\{a,b,c\}$ with $x\neq y$, we get that $(1,y)\in\theta$ for all $y\in\{a,b,c\}$ with $y\neq x$. Finally pick two distinct $y,z\in\{a,b,c\}$ different than $x$. Then we have $1\wedge y = y$ and $y\wedge z = 0$, so $(0,y)\in\theta$. So we have that $0,a,b,c,1$ are all $\theta$-equivalent. I let you check that we also have that $d$ is equivalent to $1$, so that $\theta=\nabla$. Dually, one concludes that if $\theta$ contains a pair $(1,x)$ for $x\in\{a,b,c,d\}$, then $\theta=\nabla$ too.
Suppose then that $0$ is not $\theta$-equivalent to any other element of the lattice, and similarly for $1$. You can see that this implies that none of $a,b,c$ can be in the same equivalence class. The only remaining case is that $(c,d)$ is in $\Theta$, all the other blocks being singletons. You can check that this is indeed a congruence by simply enumerating cases.
This finally gives that the congruence lattice of this lattice is a 3-element chain:
$$\Delta\subset \theta\subset\nabla$$
where $\theta$ is the equivalence relation given by the blocks $\{c,d\},\{a\},\{b\},\{0\},\{1\}$.
Edit: Since you explicitly asked for the case where $\theta$ contains $(1,d)$ in your question, let me treat it here. Applying $\wedge$ with $(b,b)$, we obtain $(b,0)\in\theta$, and similarly $(a,0)\in\theta$. Since $\theta$ is transitive we have $(b,a)\in\theta$. Applying $\vee$ with $(a,0)$ we obtain $(1,a)\in\theta$. So all of $1,a,b,d,0$ are equivalent. Finally applying $\wedge$ between $(c,c)\in\theta$ and $(d,0)\in\theta$ we obtain $(c,0)\in\theta$. So $\theta$ is the full congruence.