What does it mean for a polar coordinate system to have basis vectors?

Question

So I understand that every element of a vector space can be represented uniquely by a linear combination of the basis vectors:

$v=\alpha_1v_1+\cdots+\alpha_nv_n$

Then coordinates to those basis vectors are the coefficients of that linear combination. A vector v in R^2 has the coordinates (x,y) in Cartesian means that:

$v=x\hat{i} + y\hat{j}$

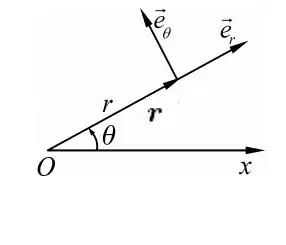
That same vector can also be described uniquely in polar coordinate by $(x,\Theta )$. The basis vectors are $\hat{r}$ and $\hat{\theta}$

But a vector in polar coordinate written in basis vectors is: $v=x\hat{r}(\theta)$. So the basis vectors are essentially not the same but depend on some $\theta$, and the coordinate $(r,\theta)$ are not the coefficients of those basis. Can anyone explain to me how we can even have non-constant basis vectors and what is the role of $\hat{\theta}$ in polar coordinate?

One way to resolve this is to think of vectors at different points $p, q$ in $\Bbb R^2$ as living in different vector spaces $T_p \Bbb R^2, T_q \Bbb R^2$. There is a canonical way to identify the vector spaces attached to different points, and under this identification what we call, e.g., $\hat i$ in one space agrees with what we call $\hat i$ in another space, but the analogous statement is not true for $\hat r$ and $\hat \theta$. — Travis Willse, Jan 24 '16 at 19:38
The map $\phi((r,\theta))=(r \cos \theta, r \sin \theta)$, induces a local coordinate system at the point $(r,\theta)$ given by $D \phi((r,\theta))= \begin{bmatrix} e_r & e_\theta \end{bmatrix}$. — copper.hat, Jan 24 '16 at 19:43
Does this help? Graphically representing vectors with polar unit vectors without converting to Cartesian coordinates — David K, Dec 10 '22 at 19:01

JorgeLRG · Answer 1 · 2022-12-30T02:06:59.313

in Cartesian coordinates a vector has two components, to go to the polar coordinates the vector has one condition, that is, the velocity vector and the acceleration vector have to be the same in both coordinates. $$\begin{aligned} \vec r &=x(t)\hat u_x+y(t)\hat u_y\\ \frac {d\vec r} {dt} &= \frac {dx} {dt}\hat u_x+\frac {dy} {dt}\hat u_y & \frac {ds} {dt} &=\sqrt{\frac {dx} {dt}^2+\frac {dx} {dt}^2}\\ \frac {d^2\vec r} {dt^2} &= \frac {d^2x} {dt^2} \hat u_x+\frac {d^2x} {dt^2} \hat u_y & |\frac {d^2\vec r} {dt^2}| &=\sqrt{\frac {d^2x} {dt^2}^2+\frac {d^2x} {dt^2}^2} \end{aligned}$$ if you find a polar function and replace $x=r(\theta)\cos\theta;y=r(\theta)\sin\theta$.
You will find that you can have speed and the magnitude of acceleration which simplify to this: $$\begin{aligned} \frac {ds} {d\theta} &= \sqrt{\frac {dr} {d\theta}^2+r^2} \\ \frac {d^2\vec r} {d\theta^2} &= \sqrt{\frac {d^2x} {d\theta^2}-2r\frac {d^2x} {d\theta^2}+r^2+4\frac {dr} {d\theta}^2} \end{aligned}$$ There is a vector in polar coordinates from which you can get these same magnitudes, and that is found with the use of derivatives of basis unit vector in polar coordinates. $$\begin{aligned} \vec r &= r(\theta) \hat e_r\\ \frac {d\vec r} {d\theta} &= \frac {dr} {d\theta}\hat e_r+r\hat e_\theta\\ \frac {d^2\vec r} {d\theta^2} &= \bigg(\frac {d^2 r} {d\theta^2}-r\bigg) \hat e_r +\frac {dr} {d\theta} \hat e_\theta \end{aligned}$$

What does it mean for a polar coordinate system to have basis vectors?

1 Answers1