5

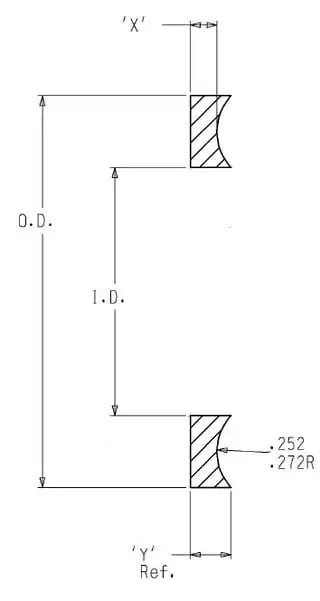
I am trying to come up with a way to calculate the cross-sectional area of the shape shown in the figure below. My first method would be to subtract the circle from the rectangle like this: $$(Y)\left(\frac{OD-ID}{2}\right)-A_{circle}$$, however, I do not know how to calculate the area of this circle since the OD and ID are not tangent to it. Also, I would prefer to use the $'X'$ dimension since $'Y'$ is a reference only.

Figure 1: Back-up ring shape

LSUEngineer
  • 53
  • Here is http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference for displaying numbers and functions. – Arbuja Jan 18 '16 at 17:41
  • 3
    We need the radius of the circle whose "lens" is the area removed from the rectangular cross-sections, and we need the common width of the rectangle and lens. At a glance the diagram seems to say the radius is $0.272$ and the width is $0.252$. Is that how you read the diagram? – hardmath Jan 18 '16 at 17:43
  • 1
    The radius of the circle is $0.252 min$, $0.272 max$. The nominal radius is $0.262$. Both numbers are the min/max radius. – LSUEngineer Jan 18 '16 at 17:47

1 Answers1

2

You’re looking for the area of a circular segment of radius $R$ and chord length $C={OD-ID\over2}$. This can be found by subtracting the area of an isosceles triangle from the area of a sector of a circle: $$A=\frac12R^2(\theta-\sin\theta),$$ where the angle $\theta$ can be found via the relationship $C=2R\sin{\frac\theta2}$.

amd
  • 55,082