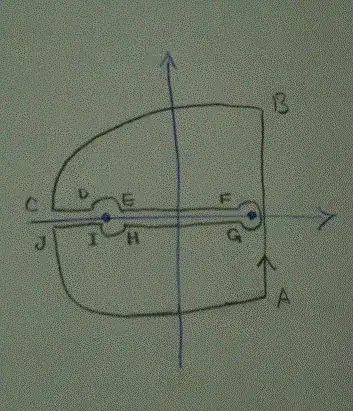
Consider the contour integral
$$\oint_C dz \frac{e^{t z}}{\sqrt{z^2-a^2}} $$
where $C$ is the contour drawn above, and $t \gt 0$. By Cauchy's theorem, this integral is zero. However, to evaluate the ILT, we need to evaluate all of the pieces of the contour integral. Thankfully, the OP has provided a diagram with such nice labels. Thus,
$$\int_{AB} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = \int_{\beta-i R}^{\beta+i R} ds \frac{e^{t s}}{\sqrt{s^2-a^2}}$$
$$\int_{BC} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = i R \int_{\pi/2}^{\pi} d\theta \, e^{i \theta} \frac{e^{t R e^{i \theta}}}{\sqrt{R^2 e^{i 2 \theta}-a^2}} $$
$$\int_{CD} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = \int_{-R}^{-a-i \epsilon} dx \frac{e^{t x}}{\sqrt{x^2-a^2}} $$
$$\int_{DE} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = i \epsilon \int_{\pi}^0 d\phi \, e^{i \phi} \frac{e^{t(-a+\epsilon e^{i \phi})}}{\sqrt{(-a+\epsilon e^{i \phi})^2-a^2}}$$
$$\int_{EF} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = \int_{-a+\epsilon}^{a-\epsilon} dx \frac{e^{t x}}{e^{i \pi/2} \sqrt{a^2-x^2}} $$
$$\int_{FG} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = i \epsilon \int_{\pi}^{-\pi} d\phi \, e^{i \phi} \frac{e^{t(a+\epsilon e^{i \phi})}}{\sqrt{(a+\epsilon e^{i \phi})^2-a^2}}$$
$$\int_{GH} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = \int_{a+\epsilon}^{-a-\epsilon} dx \frac{e^{t x}}{e^{-i \pi/2} \sqrt{a^2-x^2}} $$
$$\int_{HI} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = i \epsilon \int_{2 \pi}^{\pi} d\phi \, e^{i \phi} \frac{e^{t(-a+\epsilon e^{i \phi})}}{\sqrt{(-a+\epsilon e^{i \phi})^2-a^2}}$$
$$\int_{IJ} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = \int_{-a-i \epsilon}^{-R} dx \frac{e^{t x}}{\sqrt{x^2-a^2}} $$
$$\int_{JA} dz \frac{e^{t z}}{\sqrt{z^2-a^2}} = i R \int_{\pi}^{3 \pi/2} d\theta \, e^{i \theta} \frac{e^{t R e^{i \theta}}}{\sqrt{R^2 e^{i 2 \theta}-a^2}} $$
OK, there's a lot there, but it's not nearly as bad as it looks. The integral over $AB$ will be $i 2 \pi$ times the ILT as $R \to \infty$. The integral over $BC$ vanishes in this limit because its magnitude is bounded by
$$\frac{R}{\sqrt{R^2-a^2}} \int_0^{\pi/2} d\theta \, e^{-t R \sin{\theta}} \le \frac{R}{\sqrt{R^2-a^2}} \int_0^{\pi/2} d\theta \, e^{-2 t R \theta/\pi} \le \frac{\pi}{2 t \sqrt{R^2-a^2}}$$
The integral over $JA$ vanishes for similar reasons. The integrals over $CD$ and $IJ$ cancel each other out. The integrals over $DE$, $HI$, and $FG$ vanish as $\epsilon \to 0$. Thus, in these limits, we may write the ILT as follows:
$$\int_{\beta-i \infty}^{\beta+i \infty} ds \frac{e^{t s}}{\sqrt{s^2-a^2}} - i 2 \int_{-a}^a dx \frac{e^{t x}}{\sqrt{a^2-x^2}} = 0$$
or
$$\frac1{i 2 \pi} \int_{\beta-i \infty}^{\beta+i \infty} ds \frac{e^{t s}}{\sqrt{s^2-a^2}} = \frac1{\pi} \int_{-a}^a dx \frac{e^{t x}}{\sqrt{a^2-x^2}} $$
We may evaluate the integral on the RHS as follows. Sub $x=a \cos{u}$; then the integral is equal to
$$\frac1{\pi} \int_0^{\pi} du \, e^{a t \cos{u}} = I_0(a t)$$
where $I_0$ is the modified Bessel function of the first kind of zeroth order. Thus,
$$\frac1{i 2 \pi} \int_{\beta-i \infty}^{\beta+i \infty} ds \frac{e^{t s}}{\sqrt{s^2-a^2}} = I_0(a t)$$